Poznajemy elementy indukcyjne – część 2

W tym odcinku  zamieszczone są dalsze informacje o elementach indukcyjnych i jest on kontynuacją poprzedniego artykułu. Dodatkowo podano pokrewne wiadomości dotyczące kondensatorów.

Cewka w praktyce

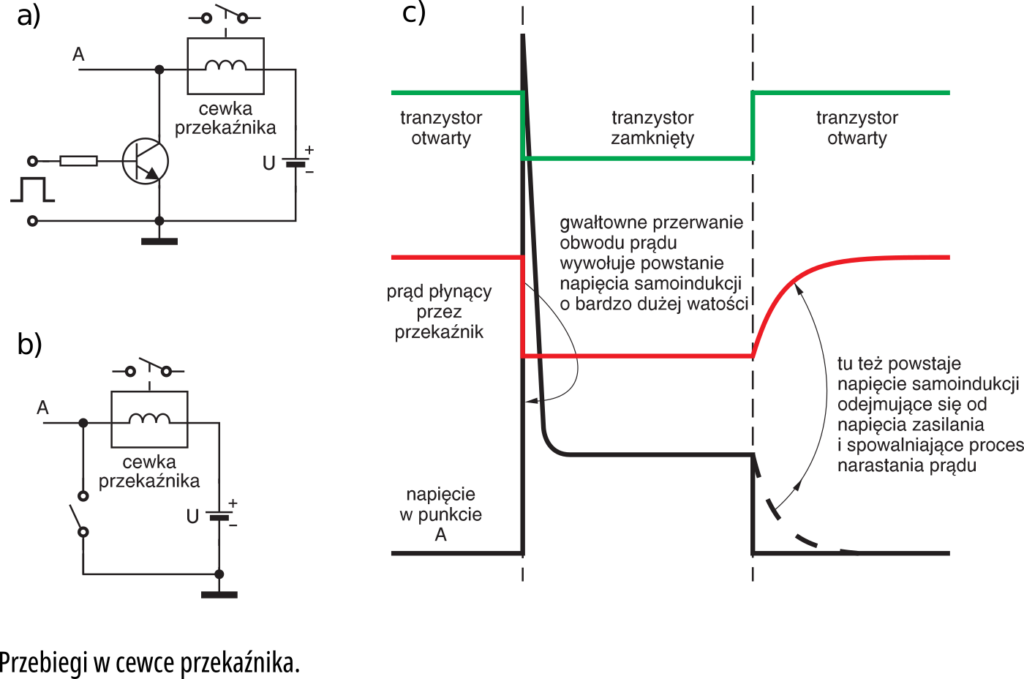
Zobaczmy teraz, jak zasady podane w poprzednim odcinku przejawiają się w typowym układzie sterowania przekaźnika, pokazanym na rysunku 1a. Ponieważ tranzystor pełni tu tylko funkcję włącznika, można układ przedstawić, jak na rysunku 1b.

Najpierw załóżmy, że tranzystor przewodzi i przez cewkę przekaźnika płynie prąd. W cewce tej zostaje więc zgromadzona pewna ilość energii. Co dzieje się po zatkaniu tranzystora, czyli przerwaniu obwodu? Jak wiemy, cewka przeciwstawia się zmianom prądu. Cewka „chciałaby”, żeby dalej płynął przez nią prąd, dlatego indukuje się na niej napięcie. Ponieważ prąd „nie może sobie znaleźć” nowej drogi przepływu, na cewce pojawia się napięcie o bardzo dużej wartości, które „usiłuje” znaleźć jakąkolwiek drogę przepływu prądu. Napięcie to może mieć wartość rzędu setek woltów i oczywiście może uszkodzić tranzystor.

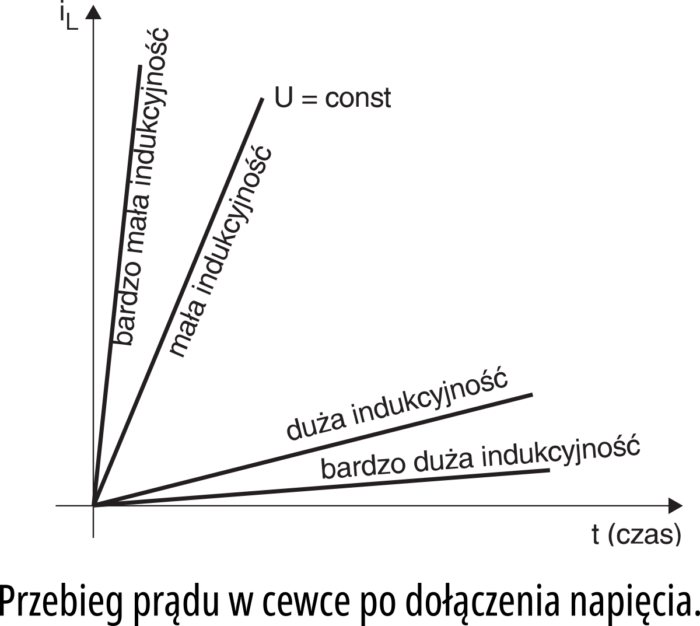
A co dzieje się po włączeniu tranzystora? W obwodzie przekaźnika pojawia się prąd. Tak, ale nie od razu − ze względu na indukcyjność uzwojenia prąd narasta stopniowo. W wielkim uproszczeniu można to sobie wyobrazić następująco: pojawiający się w pierwszej chwili po włączeniu mały prąd, powoduje powstanie na cewce napięcia o wartości niemal równej napięciu zasilającemu i takim kierunku, że niejako znosi ono napięcie zasilające. Ponieważ indukcyjność cewki przekaźnika (a tym samym ilość możliwej do zmagazynowania energii) jest stosunkowo niewielka, napięcie samoindukcji stopniowo zmniejsza się, a prąd rośnie do ustalonej wartości, wyznaczonej przez rezystancję uzwojenia. Przebiegi napięć i prądów pokazuje rysunek 1c.

Inaczej jest, gdy równolegle z cewką włączona jest dioda − jak na rysunku 2a. Podczas działania przekaźnika jest ona spolaryzowana w kierunku zaporowym i prąd przez nią nie płynie. Prąd i1 płynie w obwodzie: bateria − przekaźnik − tranzystor (klucz) − bateria. Po wyłączeniu tranzystora, prąd „chce” nadal płynąć przez cewkę przekaźnika, więc na cewce indukuje się napięcie. Tym razem będzie to napięcie rzędu 0,6…0,7 V − tylko tyle wystarczy, aby prąd „znalazł” nową drogę przepływu − prąd i2 popłynie przez diodę. Przebiegi napięć i prądów pokazane są na rysunku 2b. A teraz przekonaj się, iż w cewce można zmagazynować tylko niewielką ilość energii. Podłącz w szereg z taką diodą jakąkolwiek diodę LED (ale nie stosuj LEDa zamiast tej diody) i zobacz jak krótki jest błysk przy przerywaniu obwodu.

Czy teraz jesteś przekonany, że w obwodzie z tranzystorem zawsze należy włączać diodę równolegle do cewki przekaźnika? Czy potrafisz odpowiedzieć na pytanie, dlaczego maksymalny chwilowy prąd płynący przez tę diodę nie jest większy niż prąd pracy przekaźnika?

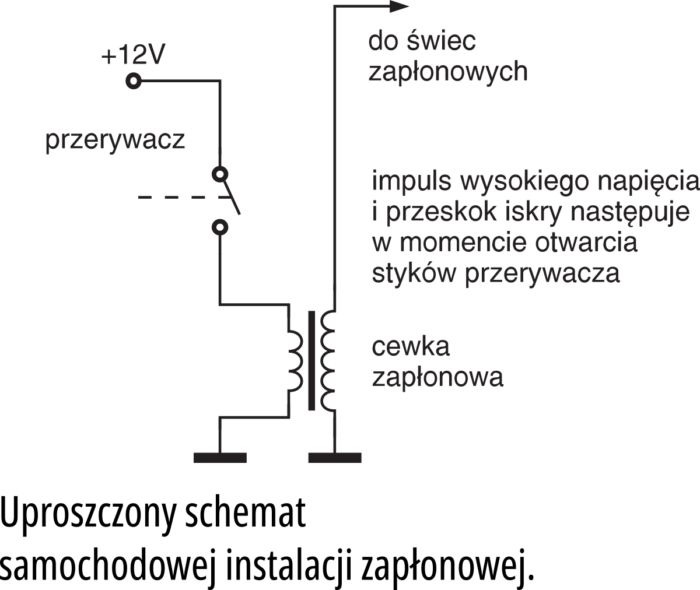
Czy rozumiesz działanie cewki wysokiego napięcia w samochodzie, gdy po przerwaniu przepływu prądu występuje przepięcie o wartości wielu tysięcy woltów, wywołujące przeskok iskry między elektrodami świecy? Uproszczony schemat instalacji zapłonowej samochodu pokazany jest na rysunku 3. Dla zwiększenia napięcia wyjściowego, zamiast pojedynczej cewki stosuje się tu transformator, czyli dwa uzwojenia o różnej liczbie zwojów.

Stała czasowa

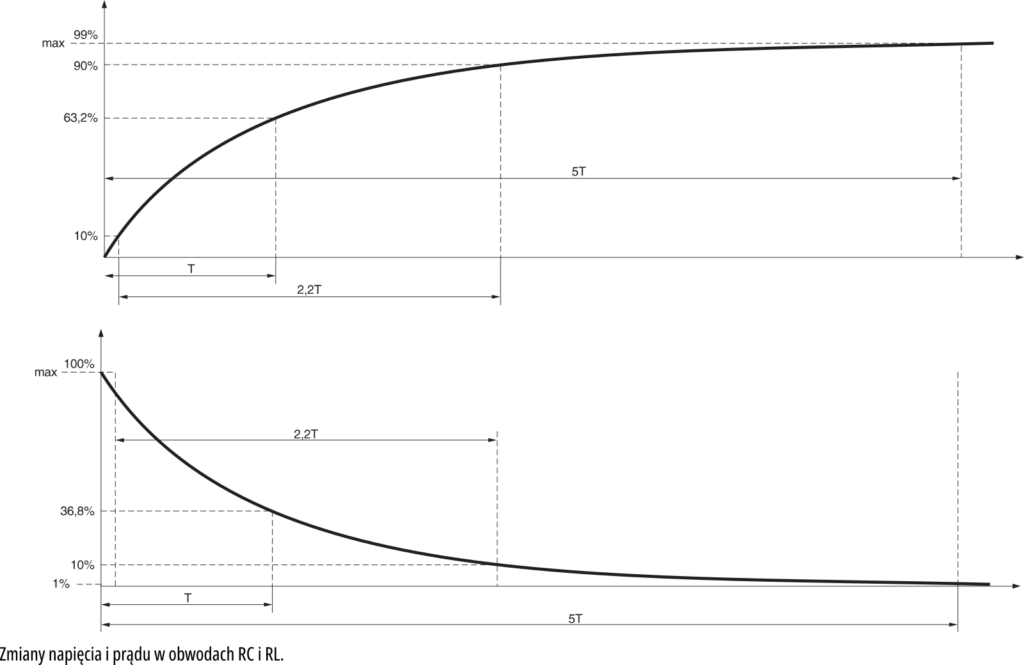
Czy pamiętasz ze szkoły przebiegi takie, jak na rysunku 4? Popatrz jeszcze raz na rysunek 1 w poprzedniej części i zauważ, że przebiegi z rysunku 4 obrazują zmiany ciśnienia i przepływu wody na zwężkach 2, 4, oraz na turbinie biernej i pionowej rurze po otwarciu zaworu głównego. Oczywiście przedstawiają one także zmiany prądu i napięcia w obwodach z kondensatorem C i cewką L z rysunku 2 w poprzedniej części po zwarciu wyłącznika S1. Sam określ, która krzywa przedstawia przebieg zmian napięcia, a która zmian prądu kondensatora. A jak ma się sprawa z cewką?

Załóżmy teraz, iż mamy dwa kondensatory o różnych pojemnościach.

Kondensatory ładujemy do jakiegoś napięcia. Zgodnie z podanym wcześniej wzorem, w kondensatorach zgromadzi się pewna ilość energii. Jeśli teraz do obu kondensatorów dołączymy jednakowe rezystory, to popłynie przez nie prąd. Napięcia na kondensatorach i prąd płynący przez rezystory będą zmieniać się w czasie tak, jak pokazuje to rysunek 4b. Jest oczywiste, że w obwodzie z kondensatorem o większej pojemności, gdzie gromadzi się więcej energii, przepływ prądu będzie trwał dłużej.

Podobny eksperyment można też przeprowadzić z dwoma różnymi cewkami: jeśli podłączymy napięcie do szeregowego obwodu RL, to prąd będzie narastał stopniowo, a na cewce pojawi się skok napięcia o czasie trwania zależnym od indukcyjności tej cewki i od współpracującej rezystancji.

W praktyce częściej interesuje nas nie tyle ilość zgromadzonej energii, co czas ładowania lub rozładowania przez daną rezystancję. Zamiast więc liczyć energię, mierzyć napięcia, korzystniej jest wprowadzić dodatkową wielkość, trafnie charakteryzującą każdy obwód składający się z rezystora i kondensatora (obwód RC) lub rezystora i cewki (obwód RL). Tą wielkością jest tak zwana stała czasowa, oznaczana T lub t:

T = R C

T = L/R

Zauważ, że stała czasowa jest niezależna od napięcia. Wydaje się, iż potrafimy łatwo obliczyć, przez ile czasu w obwodzie RC lub RL będzie płynął prąd.

Ale o jaki czas tu chodzi? Jak widać z rysunku 4 nie możemy mówić o spadku napięcia czy prądu od wartości maksymalnej do zera (albo o wzroście od zera do wartości maksymalnej). Prąd i napięcie nie zmieniają się liniowo, tylko wykładniczo, a odpowiednią zależność dla kondensatora wyrażają wzory, których być może nie bardzo rozumiesz i którymi na razie nie musisz zaprzątać sobie głowy:

u = U e^−t/RC

lub

u = U e^−t/T

Podobny wzór można podać dla indukcyjności

We wzorach tych występuje liczba e − podstawa logarytmów naturalnych. Właśnie z tą liczbą wiąże się dziwna wartość 0,368 i 0,632 (1 − 0,368) spotykana w większości podręczników. Właśnie po czasie T, napięcie czy prąd w obwodzie osiągnie podane 0,632 lub 0,367 wartości maksymalnej.

W praktyce, w obwodach czasowych nie stosuje się obwodów RL, więc i wzoru na stałą czasową T = L/R używa się rzadko − nie musisz go nawet pamiętać.

Natomiast bardzo często, na przykład w technice cyfrowej, stosujemy obwody RC dla uzyskania opóźnień lub wytwarzania impulsów. Uzyskane czasy nie są wcale równe stałej RC, a to ze względu na różne poziomy przełączania użytych układów scalonych. Miej świadomość, że stała czasowa T = R C wynika z zależności matematycznych i nie można jej wprost stosować do wszelkich praktycznych układów zawierających elementy RC. Pokazuje ona w przybliżeniu, jakiego rzędu czasy można uzyskać stosując dane elementy R C. Sprawdź to praktycznie − dwa generatory z rysunku 5 zawierające te same elementy RC będą wytwarzać znacznie różniące się częstotliwości. Spróbuj sam wyjaśnić przyczynę.

Powinieneś jednak wiedzieć, że na przykład po czasie 5T (5RC) napięcie lub prąd różni się od wartości końcowej (ustalonej) nie więcej niż o 1%. W przyszłości zapewne przyda ci się informacja, że w obwodzie RC, aby sygnał zmienił się od 10% do 90% jego wartości końcowej, potrzeba 2,2T (2,2RC) czasu. Zależności te zobaczysz na rysunku 4.

Na razie wystarczy żebyś wiedział, że w praktyce obwody RC stosuje się do wytwarzania i opóźniania przebiegów impulsowych. W przyszłości dowiesz się, iż kondensatory (a teoretycznie także cewki) mogą być używane do przeprowadzania ważnych operacji matematycznych: całkowania i różniczkowania. Zapewne w podręcznikach spotkałeś stosowne wzory. Teraz nie zawracaj sobie tym głowy. Kiedyś wyjaśnię ci to przy omawianiu wzmacniaczy operacyjnych.

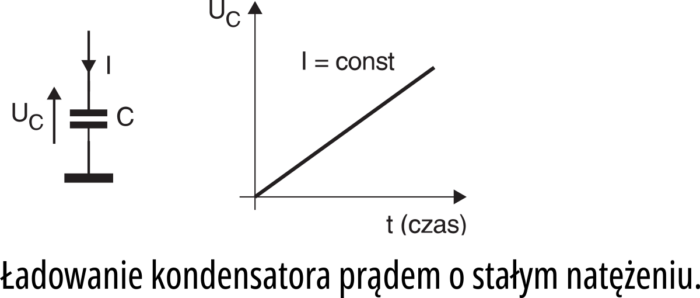
Na całkach i różniczkach znać się na razie nie musisz, ale zapamiętaj ważny wzór praktyczny, który z pewnością w przyszłości ci się przyda: C×U = I×t

Wzór ten dotyczy sytuacji, gdy kondensator jest ładowany (lub rozładowywany) prądem I o stałym natężeniu − zobacz rysunek 6.

Oczywiście napięcie na kondensatorze zmienia się wtedy liniowo. Przekształcając wzór możesz obliczyć o ile zmieni się napięcie na kondensatorze o pojemności C po czasie t, gdy prąd ładowania (rozładowania) ma wartość I:

lub też ile czasu potrzeba, aby napięcie zmieniło się o wartość U:

Pomyśl teraz, co będzie się działo z prądem, jeśli do danej cewki dołączymy napięcie? Jeśli cewka będzie zawierała wiele zwojów cienkiego drutu (czyli oprócz indukcyjności będzie mieć znaczną rezystancję), wtedy możemy potraktować ją jako połączenie indukcyjności L i rezystancji uzwojenia R (na przykład cewka przekaźnika celowo ma znaczną rezystancję). Schemat zastępczy rzeczywistej cewki pokazany jest na rysunku 7. Oczywiście prąd będzie narastał, jak na rysunku 4a. Ale większość cewek ma stosunkowo małą rezystancję. Dla uproszczenia załóżmy, że rezystancja cewki jest równa zeru. Jak wtedy zmieniać się będzie prąd? Pomyśl!

Masz rację! Prąd będzie wzrastał liniowo (teoretycznie aż do nieskończoności). Pokazuje to rysunek 8. Podaję ci następny wzór: L×I = U×t

Nie musisz go pamiętać, jest rzadko wykorzystywany w praktyce. Podana zależność umożliwia jednak stosunkowo prosty pomiar indukcyjności cewki:

Wystarczy dołączyć do cewki napięcie o znanej wartości i obserwować (np. za pomocą oscyloskopu) szybkość narastania prądu − porównaj rysunek 9.

Cewki kontra kondensatory

Na podstawie podanych wiadomości i wzorów mogłeś się przekonać, że cewki i kondensatory są „blisko spokrewnione” Na pewno spotkałeś się już z potocznym i mało precyzyjnym stwierdzeniem, że „z cewkami sprawa ma się tak samo, jak z kondensatorami, tylko odwrotnie”. Coś w tym jest − rzeczywiście zależności i wzory opisujące oba te elementy są bardzo podobne − spróbuj to teraz wyczuć intuicyjnie.

Nie masz chyba wątpliwości, że kondensator przeciwstawia się zmianom napięcia, i na próbę zmiany napięcia reaguje gwałtowną zmianą prądu. Jeśli spróbujesz gwałtownie zmienić napięcie na kondensatorze (na przykład dołączając źródło napięcia, czy też zwierając wyprowadzenia naładowanego kondensatora), wtedy przez kondensator popłynie bardzo duży prąd. Jest to chyba dla ciebie oczywiste, że taki chwilowy prąd ładowania czy rozładowania może być wielokrotnie większy niż jakiś mały prąd, którym w jakimś układzie, w normalnych warunkach pracy, ładujemy lub rozładowujemy kondensator. Analogicznie jest z cewką − na próbę zmiany wartości, czy kierunku prądu, odpowiada ona zmianami napięcia.

Przemyśl to dokładnie. Porównaj też podane wzory i zauważ ich podobieństwo.

Obwód napięcia zmiennego

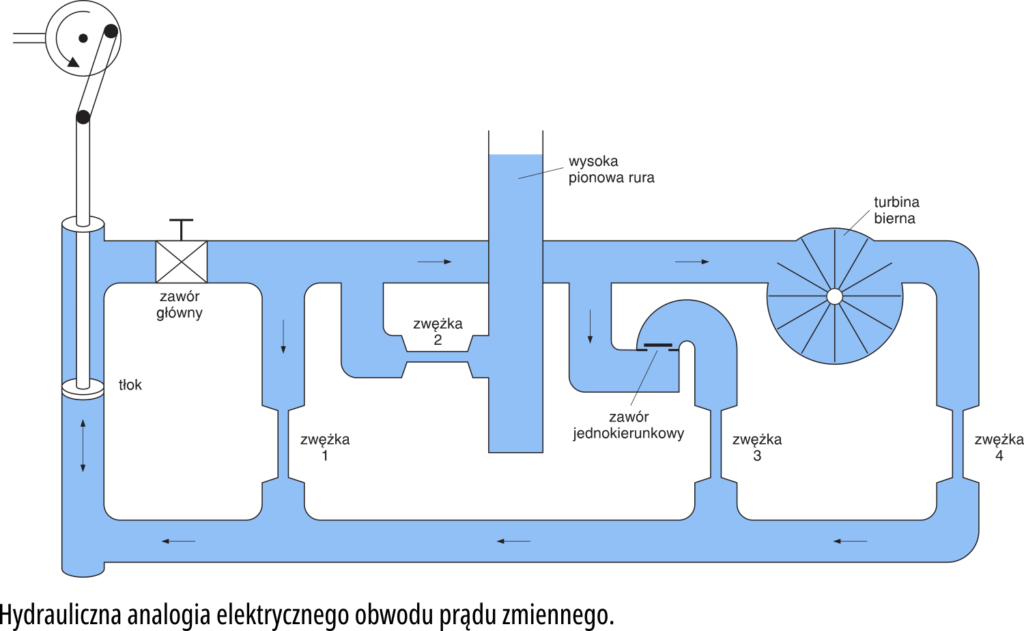
Do tej pory zajmowaliśmy się obwodem napięcia stałego. Ale model hydrauliczny równie dobrze ilustruje również zachowanie cewki i kondensatora przy prądzie zmiennym. Musimy tylko znaleźć element reprezentujący źródło napięcia zmiennego. Popatrz na rysunek 10. Pompę zębatą zastąpiliśmy cylindrem z tłokiem. Tłok, napędzany silnikiem z odpowiednią przekładnią, porusza się w cylindrze ruchem posuwisto−zwrotnym. Wzrost ciśnienia na jednym wylocie cylindra związany jest ze spadkiem ciśnienia na drugim wylocie.

W obwodzie, jak na rysunku 10, woda nie płynie więc w jednym kierunku − cząsteczki wody drgają, przesuwając się w obydwie strony od położenia spoczynkowego. Zmiany ciśnienia w czasie określone są funkcją sinusoidalną, jak na rysunku 11. Ich drgania dobrze przedstawiają zachowanie nośników prądu, czyli elektronów, w przewodach obwodu prądu zmiennego. Jakie to proste, prawda?

No tak, ale spostrzegawczy Czytelnik zauważy, że coś z naszą analogią jest nie w porządku. Skąd mianowicie ma się brać woda do napełnienia rury z rysunku 10? Jeśli to zauważyłeś, gratuluję spostrzegawczości!

Rzeczywiście analogia nie jest zupełna, ale nie w tym problem; dzięki temu spostrzeżeniu wyjaśnimy jeszcze pojęcie napięcia ujemnego, masy i uziemienia.

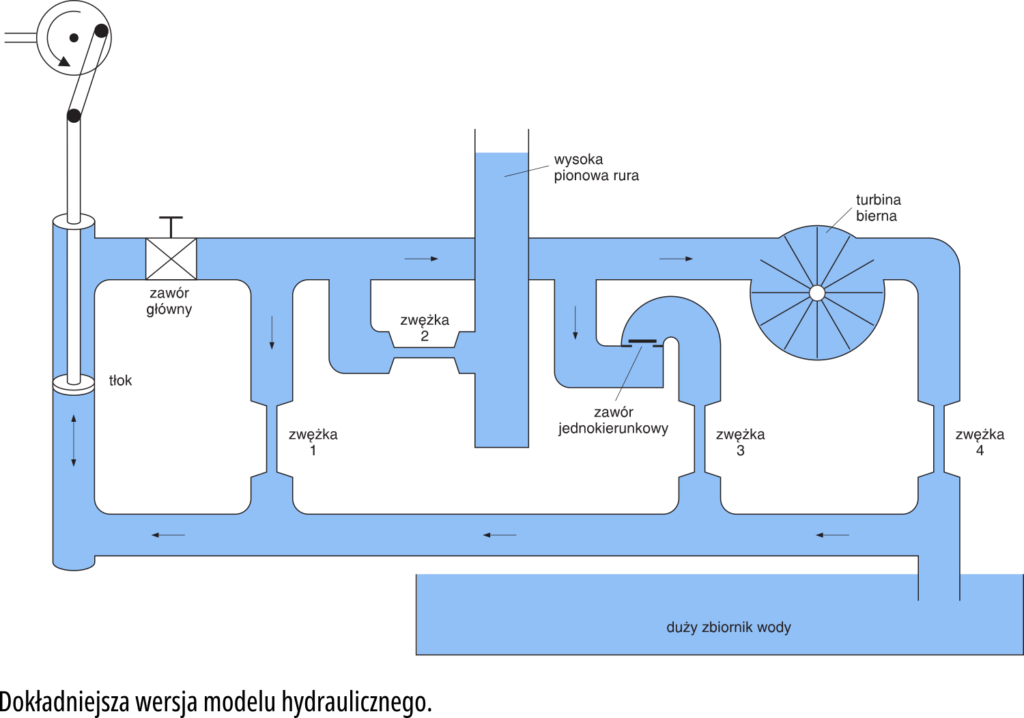
Poparz na rysunek 12. Tym razem wyobrażamy sobie, że nasz system hydrauliczny umieszczony jest na poziomie morza i otwarty koniec dolnej rury jest zanurzony w wodzie. Niezależnie od tego, ile litrów wody dolejemy do morza, albo ile z niego pobierzemy, poziom wody w morzu praktycznie się nie zmieni. Poziom wody w morzu i odpowiadające mu ciśnienie przyjmujemy więc jako ciśnienie początkowe, ciśnienie odniesienia. Dokładnie tak samo wygląda sprawa z napięciem − nasza planeta, Ziemia, z grubsza biorąc, przewodzi prąd elektryczny. I tak samo jak poziom morza i panujące tam ciśnienie przyjęliśmy jako wartość odniesienia, tak też potencjał Ziemi przyjmujemy jako punkt odniesienia dla napięć elektrycznych. Mówimy więc o napięciach mierzonych w stosunku do ziemi (tym razem pisanej już małą literą). Teraz nie ma już problemu: rysunek 12 nie budzi zastrzeżeń.

Jeśli tłok porusza się do góry (na rysunku), na górnym wylocie cylindra ciśnienie jest większe niż ciśnienie odniesienia w morzu. A gdy tłok porusza się do dołu i znajduje się w dolnej części cylindra, ciśnienie na górnym wylocie jest mniejsze (!) niż ciśnienie odniesienia. Chyba nie widzisz tu problemu − jest to po prostu podciśnienie − cząsteczki wody są wtedy wyciągane z morza (to podciśnienie odpowiada oczywiście ujemnemu napięciu elektrycznemu).

Jak więc zachowają się odpowiedniki cewki i kondensatora przy prądzie przemiennym? Popatrz na rysunek 12 i jego elektryczny odpowiednik na rysunku 13.

Załóżmy, że tłok wykonuje określoną i stałą liczbę cykli roboczych w ciągu minuty. Gdy ciśnienie na (górnym) wylocie cylindra jest dodatnie, woda jest wpychana przez zwężkę 2 do pionowej rury i jej poziom wzrasta. Gdy tłok przesuwa się na dół i ciśnienie na wylocie jest mniejsze niż ciśnienie w rurze, woda jest z rury wyciągana. Poziom wody w rurze (napięcie na kondensatorze) waha się w rytm ruchów tłoka (zmian napięcia generatora). Gdy zwiększymy średnicę rury (pojemność kondensatora), wtedy przy tej samej zwężce (rezystorze R2) zmiany poziomu wody w rurze (napięcia kondensatora), będą oczywiście mniejsze. Tak samo zmiany poziomu wody (napięcia na kondensatorze) będą mniejsze, gdy zwiększymy częstotliwość ruchów tłoka (częstotliwość zmian napięcia generatora).

Odwrotnie będzie z turbiną (cewką). Przy małym kole zamachowym (indukcyjności), przez turbinę (cewkę) będzie przepływał znaczny prąd. Po prostu turbina o małej bezwładności będzie się obracać raz w jedną, raz w drugą stronę w rytm zmian ciśnienia zasilającego. Gdy jednak bezwładność będzie bardzo duża, to prąd przez nią przepływający będzie znikomo mały − w czasie jednego cyklu ciężka turbina nie zdąży nawet drgnąć.

Tak samo przy zwiększeniu częstotliwości pracy tłoka, ilość wody przepływająca przez daną turbinę na pewno się zmniejszy.

Dokładnie ilustruje to zachowanie cewki przy prądzie zmiennym. Czym większa indukcyjność, tym mniejszy prąd, tak samo czym większa częstotliwość tym mniejszy prąd.

Zauważ w tym miejscu, że przy prądzie stałym mówiliśmy, iż kondensator i cewka przeciwstawiają się zmianom (napięcia i prądu), a teraz możemy mówić o oporności cewki i kondensatora w obwodach prądu przemiennego. Opór taki nazywamy reaktancją (pojemnościową i indukcyjną) i dla odróżnienia od rezystancji R (która występuje i przy prądzie stałym, i przy zmiennym) jest oznaczany odpowiednio: XC oraz XL. A oto stosowne wzory, które musisz zapamiętać, bo będziesz ich wielokrotnie używał:

gdzie f − częstotliwość przebiegu zmiennego.

W praktyce, zamiast podawać częstotliwość w hercach, a pojemność i indukcyjność w faradach i henrach, podaje się częstotliwość w megahercach, pojemność w mikrofaradach, indukcyjność w mikrohenrach − wynik (reaktancja) wychodzi w omach. Często też podaje się pojemność w mikrofaradach a częstotliwość w kilohercach − wtedy reaktancja wyrażona jest w kiloomach.

Jak widać ze wzorów, opór cewki czy kondensatora nie jest stały. W przypadku cewki jest wprost proporcjonalny do indukcyjności tej cewki i częstotliwości prądu −rośnie ze wzrostem częstotliwości. Cewka dławi więc przepływ prądu zmiennego − dlatego cewki, które w układach mają zmniejszać przepływ prądów zmiennych, nazywamy dławikami.

W praktyce podane wzory wygodniej jest przedstawić w postaci:

Bardzo często potrzebne są też wzory na obliczenie pojemności czy indukcyjności o danej reaktancji:

Do tej pory na przykładzie modelu hydraulicznego przedstawiłem Ci najważniejsze informacje o cewkach i kondensatorach. Jeśli jesteś dociekliwy, spróbuj jeszcze na podstawie tego modelu dociec, dlaczego mówi się, że w obwodzie zawierającym cewkę prąd opóźnia się względem przyłożonego napięcia (żartobliwa odpowiedź brzmi: ponieważ zaplątuje się w zwojach). Tak samo zastanów się co właściwie znaczy, że w obwodzie z kondensatorem prąd wyprzedza napięcie. Podpowiem Ci tylko, że chodzi o zachowanie tych elementów przy zmianach napięcia. Spróbuj narysować przebiegi prądu w cewce i kondensatorze przy dołączeniu do nich napięcia sinusoidalnego.

Podsumowujemy:
1. W cewce i kondensatorze można zgromadzić pewną ilość energii i potem tę energię odzyskać.
2. Pojemność kondensatora przeciwstawia się zmianom napięcia.
3. Indukcyjność cewki przeciwstawia się zmianom prądu. Nieodłącznym skutkiem tego zjawiska jest samoczynne wytwarzanie prądów (w kondensatorach) oraz napięć (w cewkach), których wartość może być bardzo duża.
4. W obwodach prądu przemiennego cewki i kondensatory stawiają przepływowi prądu pewien opór, który nazywamy reaktancją. Opór ten zależy od częstotliwości.

Następny odcinek znajdziesz tutaj.

Piotr Górecki