PKE – Praktyczny Kurs Elektroniki (9) Klaskacz
Na fotografii tytułowej pokazany jest model Klaskacza. Ten wyjątkowo atrakcyjny, praktyczny i zaskakująco prosty projekt wprawi w zdumienie kolegów i rodzinę. Jak najbardziej może też znaleźć praktyczne zastosowanie.
Klaskacz to dźwiękowy układ zdalnego sterowania za pomocą klaśnięcia w dłonie. Każde klaśniecie włącza/wyłącza przekaźnik i zmienia kolor świecenia diody LED. Układ reaguje na „ostre”, wysokie dźwięki, natomiast praktycznie nie reaguje na „normalne” dźwięki (mowa, muzyka).
Opis układu dla „zaawansowanych”
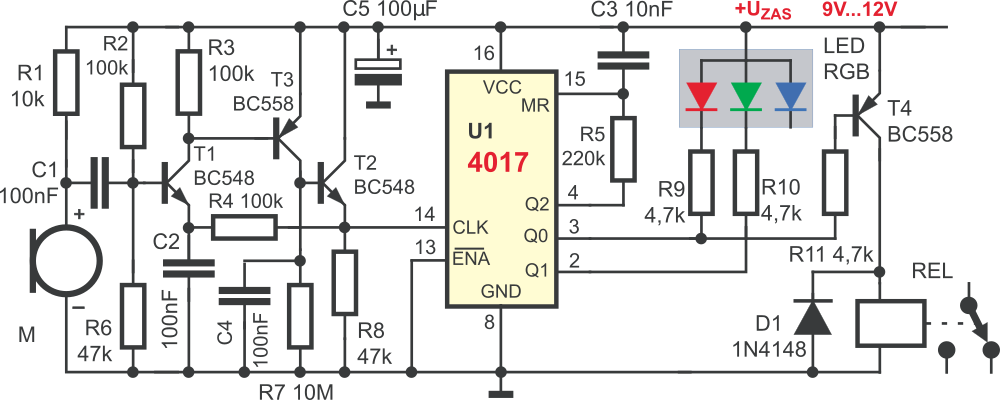
Schemat Klaskacza przedstawiony jest na rysunku A.
Układ elektroniczny składa się z dwóch głównych bloków – czujnika dźwiękowego ze wzmacniaczem z tranzystorami T1… T3 oraz tak zwanego przerzutnika T (toggle) zrealizowanego na układzie scalonym U1, na liczniku CMOS 4017. Na wejściu pracuje mikrofon elektretowy M, a elementami wykonawczymi są trzykolorowa dioda świecąca (LED RGB) oraz przekaźnik (REL). Fotografia B pokazuje z bliska mikrofon elektretowy, w którym metalowa obudowa zawsze jest połączona z wyprowadzeniem ujemnym (z masą). Jest to element biegunowy – odwrotne włączenie uniemożliwi prawidłową pracę.
Sygnał z mikrofonu elektretowego M jest wzmacniany w nietypowym wzmacniaczu tranzystorowym, który wzmacnia tylko przebiegi o wysokich częstotliwościach. Dzięki temu słabo reaguje na „normalne” dźwięki mowy czy muzyki. Dla wyższych częstotliwości akustycznych kondensator C2 stanowi niemal zwarcie, więc układ ma dla takich przebiegów duże wzmocnienie. Dla małych częstotliwości wzmacniacz ten ma wzmocnienie bliskie jedności. Pojawienie się silnego sygnału z mikrofonu, zawierającego znaczną ilość składowych o wyższych częstotliwościach, powoduje reakcję układu: dodatnie połówki sygnału z mikrofonu powodują dodatkowe otwarcie T1, a to otwiera T3. Rośnie napięcie na dwójniku R7C4. Wzmacniacz jest nietypowy, ponieważ zawiera obwód R7, C4 oraz dodatkowy bufor-wtórnik w postaci tranzystora T2. Klaśnięcie w dłonie powoduje szybkie naładowanie kondensatora C4 przez tranzystor T3, a potem powolne jego rozładowywanie przez R7. Po klaśnięciu, na rezystorze R8, a więc także na wejściu zegarowym układu 4017 (nóżka 14) występuje impuls dodatni, powodujący zmianę stanu licznika. Jednocześnie zwiększenie napięcia na R8, a w konsekwencji także na C2, powoduje zatkanie tranzystora T1, przez co wzmacniacz na czas rozładowania C4 przez R7 zostaje praktycznie wyłączony, co zapewnia prawidłową pracę licznika U1. Zasadniczo licznik 4017 zlicza do dziesięciu. W tym przypadku cykl zliczania został skrócony do dwóch stanów (0-1-0-1-itd.), a to dzięki dołączeniu wyjścia Q2 (nóżka 4) do wejścia zerującego RST (nóżka 15). Dodatkowy obwód R5C3 zapewnia wyzerowanie licznika po włączeniu zasilania. Świeci wtedy zielona struktura diody LED RGB, a przekaźnik REL jest wyłączony. Aktualny stan przerzutnika pokazuje dwukolorowa dioda LED – każde klaśnięcie w dłonie spowoduje zmianę koloru świecenia lampki i zmianę stanu przekaźnika.
Fotografia C pokazuje zmontowany model klaskacza.
Poznajemy elementy i układy elektroniczne
We wcześniejszych wykładach zaczęliśmy badać przebiegi zmienne. Wszelkie zmiany napięcia lub prądu to przebiegi zmienne. Dość często są to przebiegi jednokierunkowe: zmienia się wartość napięcia czy prądu, ale kierunek (biegunowość) się nie zmienia. W elektronice najbardziej interesują nas przebiegi okresowe, okresowe, czyli powtarzalne. Często interesują nas przebiegi okresowe przemienne, gdy zmienia się i wartość, i kierunek (biegunowość) – przykłady na rysunku 1.
Prąd przemienny płynie na przemian w jedną i drugą stronę – wygląda to bardziej na drgania – wibracje względem stanu równowagi. W elektronice mamy do czynienia z przebiegami przemiennymi o najróżniejszych kształtach, w tym prostokątnym, trójkątnym, piłokształtnym i sinusoidalnym. Często nałożone są na napięcie czy prąd stały – dlatego w praktyce bardzo często oddzielnie rozpatrujemy sytuację dla prądów i napięć stałych, a oddzielnie dla zmiennych.
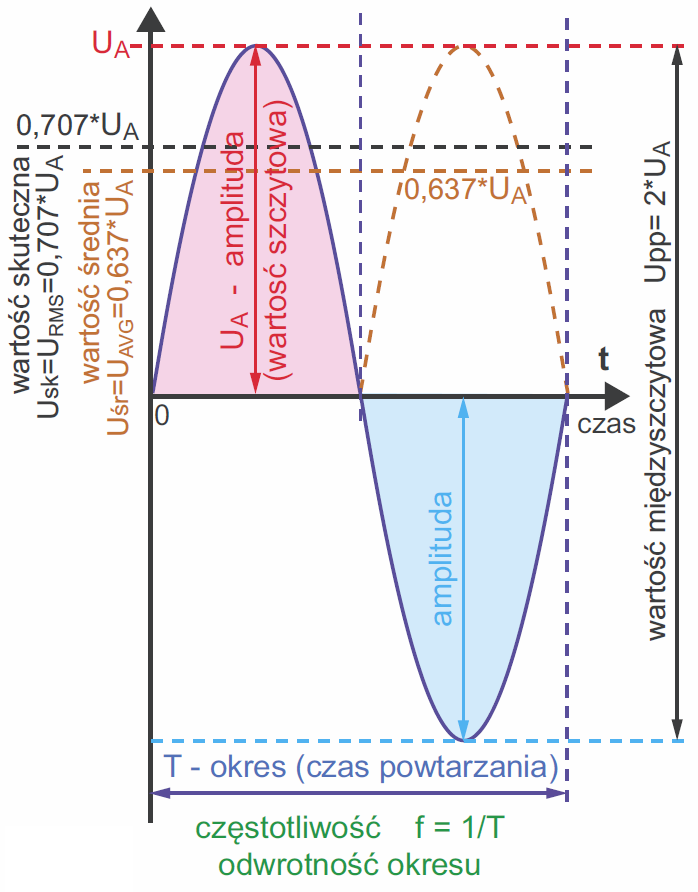
Parametry przebiegów stałych i zmiennych. Napięcia i prądy stałe charakteryzujemy bez trudu, podając ich wartość odpowiednio w woltach i amperach. Trudniej jest w przypadku przebiegów zmiennych. Przebiegi mogą mieć różne kształty, dlatego możemy też podać wartość szczytową, czyli amplitudę oraz wartość międzyszczytową. Możemy podać wartość średnią (która dla przebiegów przemiennych wynosi zero). Jednak w praktyce najważniejsza jest tak zwana wartość skuteczna (230 V napięcia sieci to właśnie wartość skuteczna), która charakteryzuje „możliwości energetyczne” przebiegu.
W przypadku przebiegów powtarzalnych, czyli okresowych, możemy podać czas – okres powtarzania w sekundach, ale zdecydowanie częściej podajemy odwrotność okresu – częstotliwość, czyli liczbę zmian na jednostkę czasu, oznaczaną f (frequency), wyrażaną w hercach (Hz). Na przykładzie sinusoidy ilustruje to rysunek 2.
Wbrew wyobrażeniom początkujących, ani przebieg prostokątny, ani trójkątny nie są ani najprostszymi, ani najważniejszymi przebiegami. Zapamiętaj, że najpopularniejsza i najważniejsza jest sinusoida, która jest przypadkiem szczególnym, wyjątkowym.
Sinusoida jest przebiegiem podstawowym, elementarnym także w tym sensie, że dowolny przebieg powtarzalny można złożyć ze składowej stałej i szeregu odpowiednio dobranych sinusoid (tzw. szereg Fouriera). W praktyce dość często robimy coś odwrotnego – przebieg złożony rozdzielamy, filtrujemy, na składową stałą i na sinusoidalne składowe zmienne. Kolejny argument, że sinusoida jest przebiegiem podstawowym, poznasz w następnym wykładzie, przy omawianiu zjawiska rezonansu.
A oto przykład kondensatora, pokazujący wyjątkowość sinusoidy: jak wspomnieliśmy wcześniej, czym większy prąd, tym szybciej ładuje/rozładowuje się kondensator. I odwrotnie: szybsze zmiany napięcia powodują przepływ większego prądu. Ponadto czym większa pojemność C, tym większy prąd płynie przy danej szybkości zmian napięcia. Zapisujemy to wzorem matematycznym i=C×du/dt, w uproszczeniu I=C×ΔU/Δt, a w jeszcze większym uproszeniu I=CU/t.
Rysunek 3 pokazuje kilka przykładów. Wielkość i kierunek prądu odpowiada szybkości i kierunkowi zmian napięcia na kondensatorze.
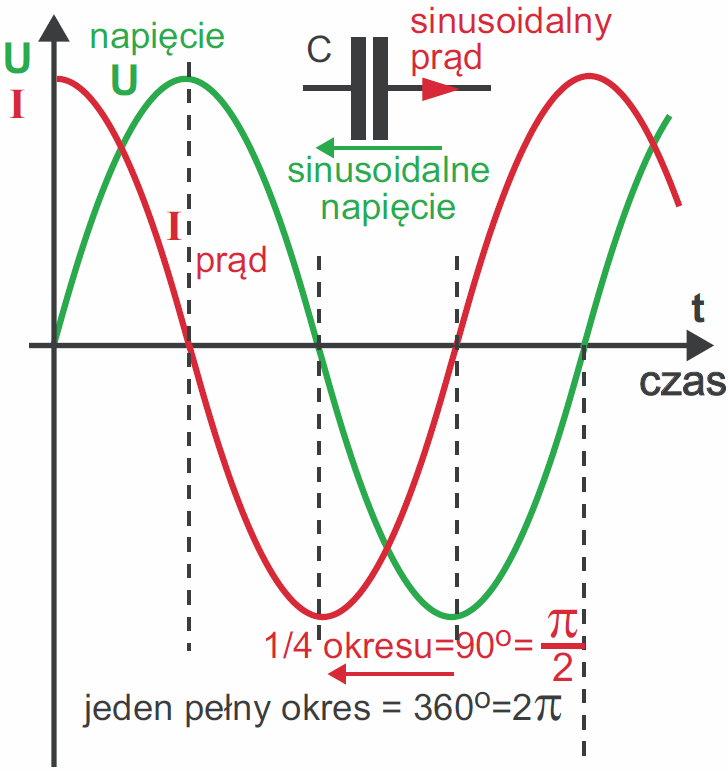
Zazwyczaj kształt przebiegu prądu jest odmienny od kształtu zmian napięcia. Jest jednak przypadek szczególny – przebieg sinusoidalny. Jeżeli na kondensatorze wystąpi napięcie o kształcie sinusoidalnym, to wtedy i prąd ma kształt sinusoidy, przy czym te sinusoidy prądu i napięcia są wzajemnie przesunięte dokładnie o jedną czwartą okresu, jak pokazuje rysunek 4.
Ponieważ sinusoida ma ścisły związek z ruchem obrotowym (jeden okres to jeden obrót, czyli 360 stopni, a w mierze kątowej 2π), przesunięcie między prądem i napięciem wyrażamy w jednostkach kąta – przesunięcie wynosi 90 stopni, czyli π/2.
Co bardzo istotne, tylko w przypadku przebiegu sinusoidalnego, gdy mamy i sinusoidalne napięcie (U), i sinusoidalny prąd (I), możemy mówić, że kondensator stanowi pewnego rodzaju oporność (U/I), nazywaną reaktancją pojemnościową, oznaczaną XC, też wyrażaną w omach. Podobnie jak przez rezystor prąd płynie według znanej zależności (I = U/R), analogicznie przez tę reaktancję płynie prąd o wartości I = U/XC, a płynący prąd I wywołuje na reaktancji XC spadek napięcia U = I×XC, gdzie U, I to wartości skuteczne sinusoidalnych (i przesuniętych) przebiegów napięcia i prądu – spójrz na rysunek rysunek 5a.
Oczywiście oporność ta zależy od pojemności kondensatora C, ale nie tylko. Oporność ta nie jest stała: czym większa częstotliwość przebiegu sinusoidalnego (f), tym reaktancja pojemnościowa XC jest mniejsza według zależności XC = 1 / 2πfC i rysunku 5b, narysowanego w skali podwójnie logarytmicznej (skali, która nie ma zera). Oporność XC jest dziwna dlatego, że prąd i napięcie w kondensatorze są wzajemnie przesunięte o kąt prosty (90 stopni), więc także reaktancja pojemnościowa XC jest w pewnym sensie „prostopadła” do rezystancji R, co początkującym wydaje się bardzo dziwne. Podkreślam, że o reaktancji pojemnościowej jako współczynniku proporcjonalności między prądem i napięciem (I=U/XC) możemy mówić tylko w przypadku przebiegów sinusoidalnych. Przy innych przebiegach zależność prądu i napięcia wyznacza podstawowy wzór i=C×du/dt.
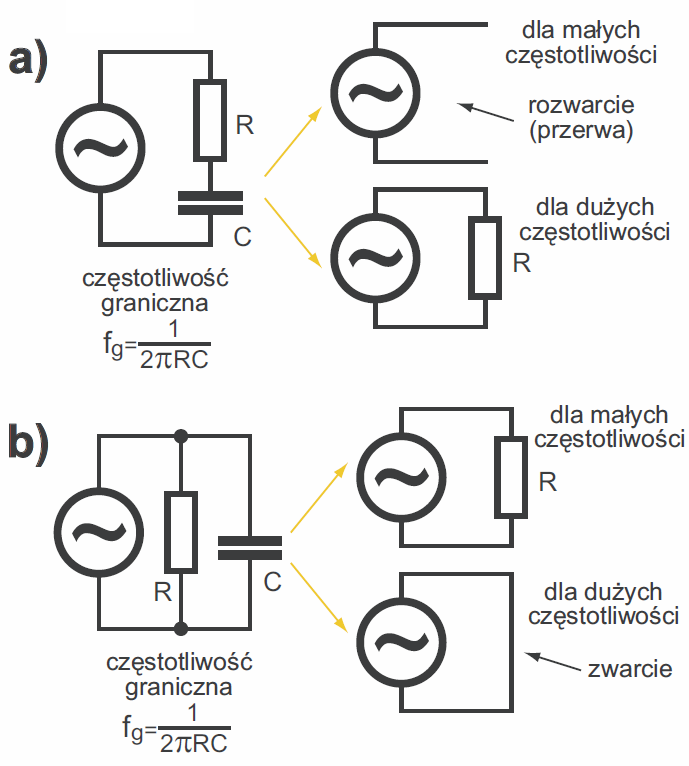
Kondensatory często pracują w obwodach filtrów sygnałów o różnych częstotliwościach. Na razie zwróć uwagę, że zgodnie ze wzorem XC=1/2πfC, dla przebiegów stałych, czyli dla przebiegów o częstotliwości f=0, kondensator ma nieskończenie wielką oporność (reaktancję) – stanowi przerwę. Z kolei przy bardzo dużych częstotliwościach kondensator ma znikomo małą reaktancję XC, co możemy traktować jako zwarcie. Takie skrajne przypadki ilustruje w uproszczeniu rysunek 6 i często właśnie tak rozumiemy obecność i rolę kondensatorów w układzie. Częstotliwość graniczna między częstotliwościami „małymi” a „dużymi” to f = 1/ 2πRC – do tego szczegółu jeszcze wrócimy.
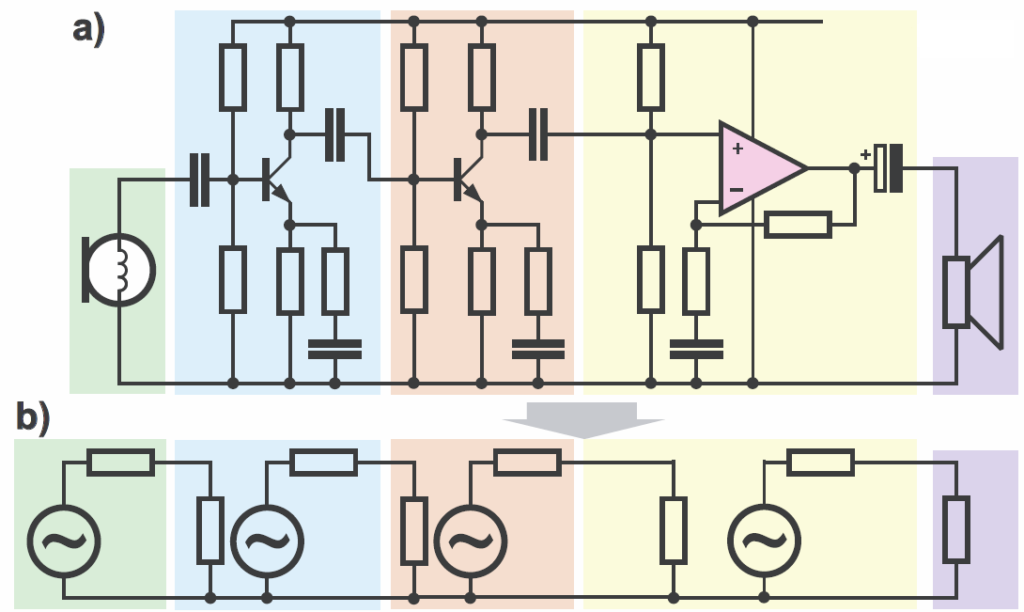
Kondensatory często wykorzystujemy do oddzielania i łączenia składowej stałej oraz składowej zmiennej. Jeżeli włączymy kondensator o odpowiednio dużej pojemności między szyny zasilania, to z punktu widzenia przebiegów zmiennych, obie szyny są zwarte, czyli dla przebiegów zmiennych zasadniczo są tym samym obwodem. I tak układ z rysunku 7a z punktu widzenia prądu stałego wygląda jak na rysunku 7b, bo pojemności są wtedy rozwarciem, przerwą. Natomiast dla wysokich częstotliwości możemy go przedstawić w nieco dziwnej postaci, jak na rysunku 7c, bo pojemności wtedy są zwarciem.
Podobnie jak kondensatory, specyficznie zachowują się też cewki. W wykładzie 6 mówiliśmy, że przy zmianach prądu cewka wytwarza napięcie samoindukcji. Miarą zdolności przeciwstawiania się zmianom prądu jest indukcyjność, oznaczana literą L, wyrażana w henrach (H). Czym szybsze zmiany prądu, tym wyższe wytwarzane napięcie samoindukcji (u= L×di/dt, w uproszczeniu U=L×ΔΙ/Δt). Zależności są podobne jak dla kondensatora (patrz rysunek 4), tylko niejako odwrotne. Niemniej analogicznie, wyłącznie przy przebiegu sinusoidalnym, i prąd, i napięcie są sinusoidalne, tylko są przesunięte „odwrotnie” niż w kondensatorze, co ilustruje rysunek 8.
Podobnie wyłącznie dla przebiegów sinusoidalnych możemy mówić o oporności cewki – o reaktancji indukcyjnej XL, której wartość określa wzór XL = 2πfL. Odwrotnie niż w kondensatorze, idealna cewka przy częstotliwości f=0, czyli dla napięć i prądów stałych, ma oporność równą zeru – stanowi zwarcie. Reaktancja rośnie ze wzrostem częstotliwości, teoretycznie do nieskończoności. W skali podwójnie logarytmicznej, analogicznie jak na rysunku 5, zmiany reaktancji cewki przedstawia linia prosta, tylko „rosnąca”. W rzeczywistości do reaktancji indukcyjnej XL dodaje się rezystancja drutu cewki, a w grę wchodzą też małe pojemności pasożytnicze, ale to odrębny, szeroki temat.
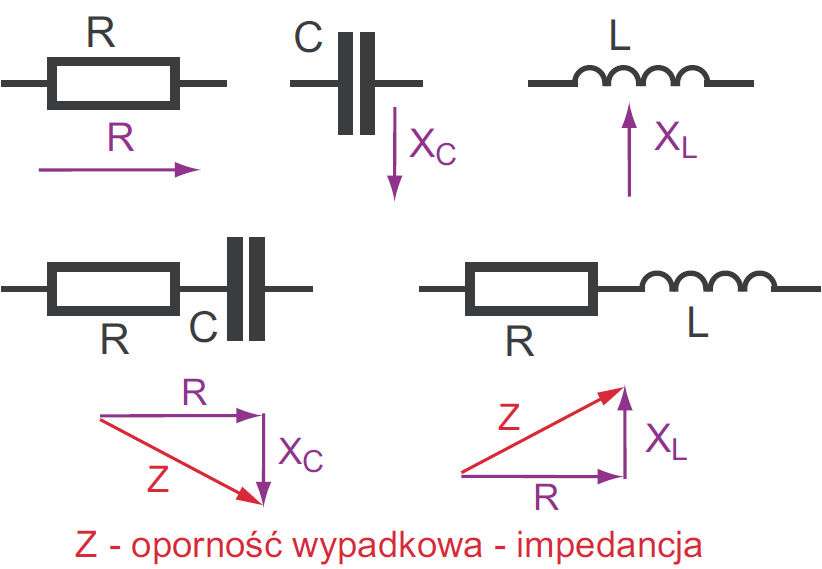
Z uwagi na przesunięcie prądu względem napięcia, także reaktancja indukcyjna XL jest w pewnym sensie prostopadła do rezystancji R, ale też odwrotna względem reaktancji pojemnościowej XC, co ilustrujemy jak na rysunku 9. Takie przedstawienie słusznie wskazuje, że z uwagi na przesunięcie napięcia i prądu, tego rodzaju oporności musimy dodawać wektorowo, a nie przez zwykłe sumowanie wartości liczbowych. Przy okazji dodajmy, że oporność wypadkowa (oporność zespolona) to impedancja, oznaczana zwykle literą Z, wyrażana w omach.
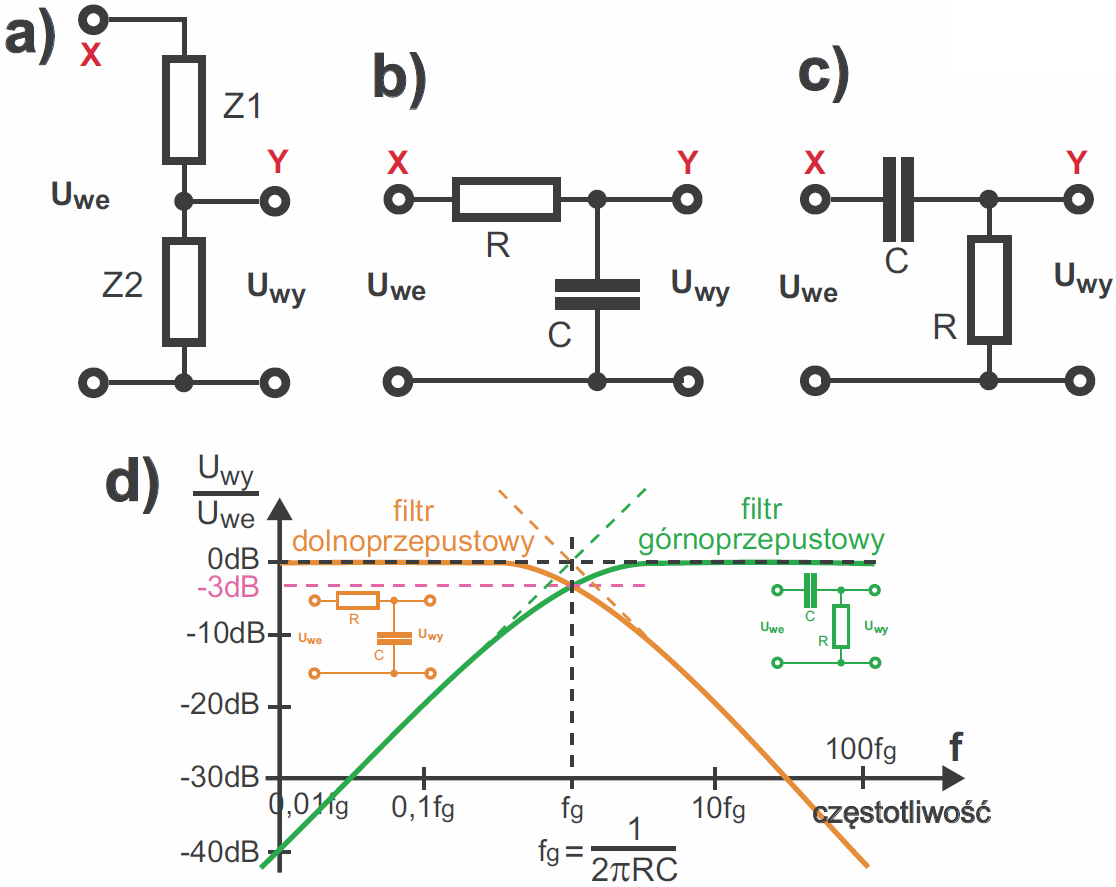
Zwróć uwagę, że łącząc szeregowo dwie dowolne impedancje ( rezystancje , reaktancje ) , otrzymujemy dzielnik napięcia – rysunek 10a. Ponieważ reaktancja XC zależy od częstotliwości, taki obwód staje się filtrem. Filtr dolnoprzepustowy z rysunku 10b tłumi wyższe częstotliwości, a filtr górnoprzepustowy z rysunku 10c przepuszcza tylko wyższe częstotliwości. Co ciekawe, przy częstotliwości granicznej f = 1/ 2πRC reaktancja pojemnościowa XC jest liczbowo równa rezystancji R, jednak z uwagi na przesunięcie fazy (rysunek 9) sygnał wyjściowy w punkcie Y ma nie 0,5, tylko 0,71 wielkości sygnału w punkcie X. Ilustruje to rysunek 10d, narysowany w skali podwójnie logarytmicznej. Zwróć uwagę, że pionowa oś jest wyskalowana w decybelach. Zasadniczo decybel to miara stosunku dwóch wielkości. Zamiast podawać stosunek Uwy/Uwe w „razach”, podajemy go w decybelach. Dla napięcia i prądu stosunek w decybelach to 20 logarytmów ze stosunku (Uwy/Uwe), podanego w „razach”. Na przykład Uwy/Uwe=10, to 20×log10, czyli 20dB, Uwy/Uwe=1000 to 60dB, a Uwy/Uwe=0,01 to –40dB.
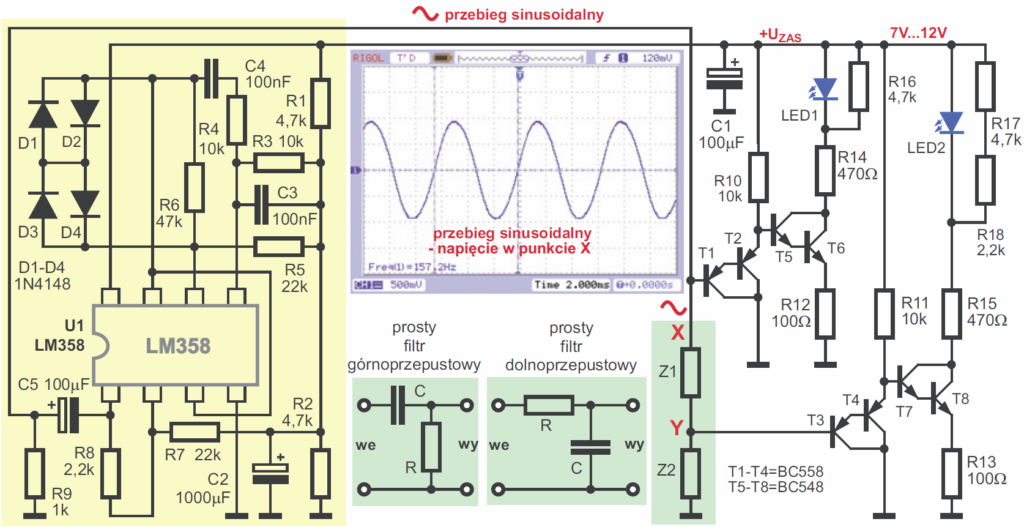
W ramach ćwiczeń na początek zbudujmy generator przebiegu sinusoidalnego i sprawdźmy omawiane wcześniej zależności. Na rysunku 11 żółtą podkładką wyróżniony jest generator sinusoidy, zrealizowany na tak zwanym wzmacniaczu operacyjnym – nie musisz na razie rozumieć, jak działa – zajmiemy się tym w przyszłości. Jak pokazuje zrzut z ekranu oscyloskopu, ten prosty generator w punkcie X wytwarza dość ładną sinusoidę o częstotliwości około 160 Hz i wartości międzyszczytowej prawie 2 Vpp (gdyby przypadkiem, wskutek fatalnego rozrzutu wartości elementów, generator nie chciał pracować, należy albo odrobinę zwiększyć wartość R6, dodając w szereg rezystor 1 kΩ…4,7 kΩ, albo nieco zmniejszyć R5, dołączając równolegle 470 kΩ…4,7 MΩ). Zieloną podkładką wyróżniony jest badany obwód – dzielnik z dowolnymi impedancjami Z1, Z2, w praktyce będzie to filtr RC. Możesz badać filtr dolno- i górnoprzepustowy.
Po prawej stronie rysunku wyróżnione są dwa jednakowe monitory napięcia, gdzie jasność świecenia diod pokazuje wielkość przebiegów na wejściu i wyjściu filtru. Rezystory R16 oraz R17 i R18 są tak dobrane, żeby przy braku kondensatora C5, czyli bez sygnału, diody LED były na progu świecenia. Obserwując jasność diod LED1, LED2, sprawdzisz, czy przebieg jest tłumiony przez filtr i na ile. Mój model pokazany jest na fotografii 12.
W miejsce Z2 wstaw rezystor 1 kΩ, a w miejsce Z1 wkładaj kolejno kondensatory 1 uF, 100 nF, 10 nF i 1 nF. Sprawdź, jak zmniejsza się jasność diody. Analogicznie zbadaj filtr dolnoprzepustowy. Możesz śmiało w bardzo szerokim zakresie zmieniać częstotliwość przebiegu generatora, wymieniając jednakowe kondensatory C=C3=C4 (1 nF…1 uF) lub jednakowe rezystory R=R3=R4 (2,2 kΩ…1 MΩ). Namęczyłem się trochę, tak dobierając wartości elementów układu, żebyś wśród pozostałych, niewykorzystanych elementów miał do dyspozycji po dwa jednakowe rezystory i kondensatory potrzebnych nominałów.
Gdy będziesz zmieniał częstotliwość generatora przez zmianę wartości R3=R4 lub C3=C4, niech Z1 i Z2 mają niezmienne wartości – obserwuj jasność diod LED przy różnych częstotliwościach przebiegu. Częstotliwość wytwarzanego przebiegu wynosi mniej więcej f = 1/2πRC
A teraz kolejne ważne zagadnienie. W podręcznikach do dziś wiele uwagi poświęca się wzmacniaczom sygnałów zmiennych ze wspólnym emiterem (OE) i ze wspólną bazą (OB). Choć dziś takie klasyczne rozwiązania wykorzystujemy bardzo rzadko, warto trochę o nich wiedzieć.
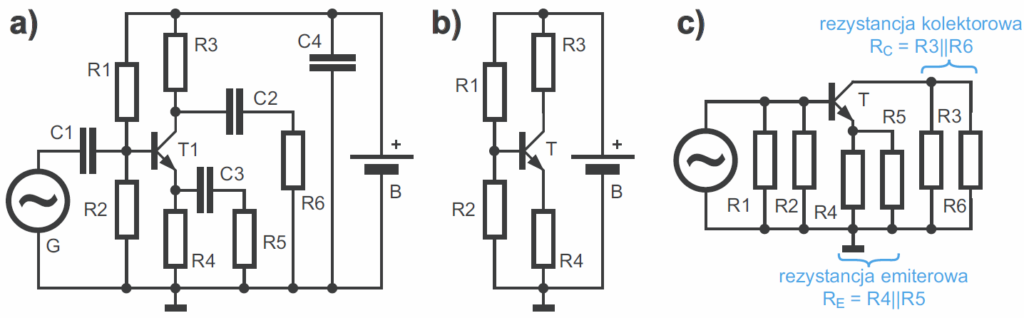
OE – wzmacniacz ze wspólnym emiterem. Tranzystor może pracować tylko przy napięciach i prądach o określonej biegunowości, więc wzmacnianie przebiegów zmiennych można zrealizować jedynie na tle napięć i prądów stałych, w najprostszym przypadku według rysunku 13. Jednak praktyczną przydatność takich wzmacniaczy całkowicie przekreśla fatalna stabilność cieplna. Zmiany temperatury złącza i napięcia UBE powodują tu duże zmiany punktu pracy, czyli prądów i napięć. Ponadto w wersji z rysunku 13a należałoby indywidualnie dobierać wartość rezystora RB, zależnie od wzmocnienia prądowego konkretnego egzemplarza tranzystora.
Najprostszym sposobem poprawy jest wprowadzenie ujemnego sprzężenia zwrotnego, co było sygnalizowane już w wykładzie 3 na rysunku 4. Czasem robi się to przez włączenie rezystora między kolektorem i bazą według rysunku 14a. Jednak częściej ujemne sprzężenie zwrotne realizuje się przez dodanie rezystora w obwodzie emitera według rysunku 14b.
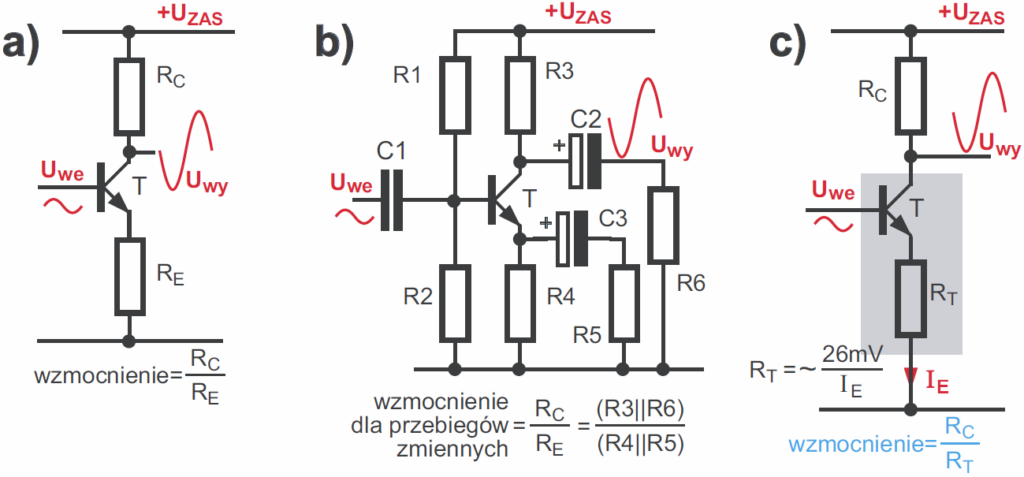
Coś za coś: ujemne sprzężenie zwrotne zwiększa stabilność punktu pracy, ale zmniejsza wzmocnienie napięciowe. Ściślej biorąc, wzmocnienie prądowe tranzystora nie zmienia się ani trochę, natomiast wzmocnienie napięciowe wyznaczone jest przez warunki pracy tranzystora. Nie wchodząc w szczegóły: dla małych sygnałów wzmocnienie to stosunek rezystancji kolektorowej RC do rezystancji emiterowej RE, co w uproszczeniu ilustruje rysunek 15a. W praktycznych układach, np. z rysunku 15b, rezystory R1…R4 decydują o stałoprądowym punkcie pracy. Natomiast dla wyższych częstotliwości kondensator C3 ma małą reaktancję XC, przez co wypadkowa rezystancja emiterowa jest mniejsza, a wzmocnienie – większe. Sytuacja wygląda jak na wcześniejszym rysunku 7c, więc wzmocnienie wyznaczone jest przez stosunek rezystancji RC/RE. Ściślej biorąc, w tranzystorze „wbudowana” jest też niewielka wewnętrzna rezystancja RT o wartości około 26 mV/IE, co ogranicza maksymalne wzmocnienie napięciowe tranzystora, jak pokazuje rysunek 15c.
Przedwzmacniacz mikrofonowy. Domowe zestawy audio zwykle mają wejście pomocnicze AUX o czułości zbyt małej, by wzmocnić malutki sygnał z mikrofonu. Aby podłączyć mikrofon, możesz zbudować dwustopniowy przedwzmacniacz według rysunku 16.
Tranzystory T1 i T2 pracują jako wzmacniacze ze wspólnym emiterem (OE). Tranzystor T3 jest wtórnikiem – buforem, przedstawionym w wykładzie 4 na rysunkach 3…7. Mikrofon elektretowy M jest elementem biegunowym i wymaga polaryzacji, stąd rezystor R2 oraz dodatkowy filtr R1C1. Fotografia 17 pokazuje mój model wraz z wtyczką typu RCA (chinch – czytaj: czincz). Wzmocnienie każdego stopnia możesz niezależnie regulować według potrzeb przez zmianę wartości R7 (220 Ω…10 kΩ) i R10 (47 Ω…2,2 kΩ). W wielu wypadkach wystarczyłby tylko jeden stopień wzmocnienia, czyli obwód z tranzystorem T2 nie byłby potrzebny (baza T3 dołączona bezpośrednio do kolektora T1). Zaznaczony szarym kolorem tranzystor T4 i dioda LED to prosty monitor – dioda powinna błyskać przy głośnych sygnałach. Taki monitor przyda się podczas uruchomiania, natomiast podczas normalnej pracy przedwzmacniacza mógłby zniekształcać najsilniejsze sygnały.
OB – wzmacniacz ze wspólną bazą. Tranzystor reaguje na zmiany napięcia UBE. Dla tranzystora nie ma znaczenia, na którą elektrodę podany zostanie sygnał. Ku zdziwieniu początkujących, elektrodą wspólną może być baza, a wejściem będzie… emiter, co w uproszczeniu pokazuje rysunek 18a.
Prąd emitera płynie teraz przez źródło sygnału, a to oznacza, że oporność wejściowa układu OB jest mała. W rzeczywistości trzeba zapewnić polaryzację stałoprądową tranzystora, na przykład według rysunku 18b. Konfiguracja OB jest często wykorzystywana przy wysokich częstotliwościowych, w rozmaitych urządzeniach radiowych. My zrealizujmy według rysunku 19 i fotografii 20 nietypowy przedwzmacniacz mikrofonowy, gdzie mikrofonem jest… jakikolwiek głośnik lub słuchawki, które zapewne znajdziesz gdzieś pod ręką.
Pierwszy stopień z tranzystorem T1 pracuje w układzie ze wspólną bazą (OB), a tranzystor T2 – w układzie OE. W tej wersji nie dodaliśmy na wyjściu wtórnika – bufora, czyli układu ze wspólnym kolektorem. Wzmocnienie możesz regulować, zmieniając wartość R7 (10 Ω…2,2 kΩ). Tranzystor T3 jest prostym monitorem – dioda LED powinna błyskać przy głośnych dźwiękach.
OC – wzmacniacz ze wspólnym kolektorem. Układ ze wspólnym kolektorem już w zasadzie omówiliśmy w wykładzie 4, gdzie analizowaliśmy różne wtórniki – bufory. Rysunek 21a pokazuje ideę i praktyczną realizację zmiennoprądowego wzmacniacza ze wspólnym kolektorem, który wprawdzie nie wzmacnia napięcia, ale niejako wzmacnia prąd i ma dużą oporność wejściową. Jeszcze większą oporność ma wtórnik z układem Darlingtona i z „podciąganiem” (bootstrap) według rysunku 21b. Spotykana jest też ulepszona wersja wtórnika ze źródłem (lustrem) prądowym w roli rezystancji RE – rysunek 21c.
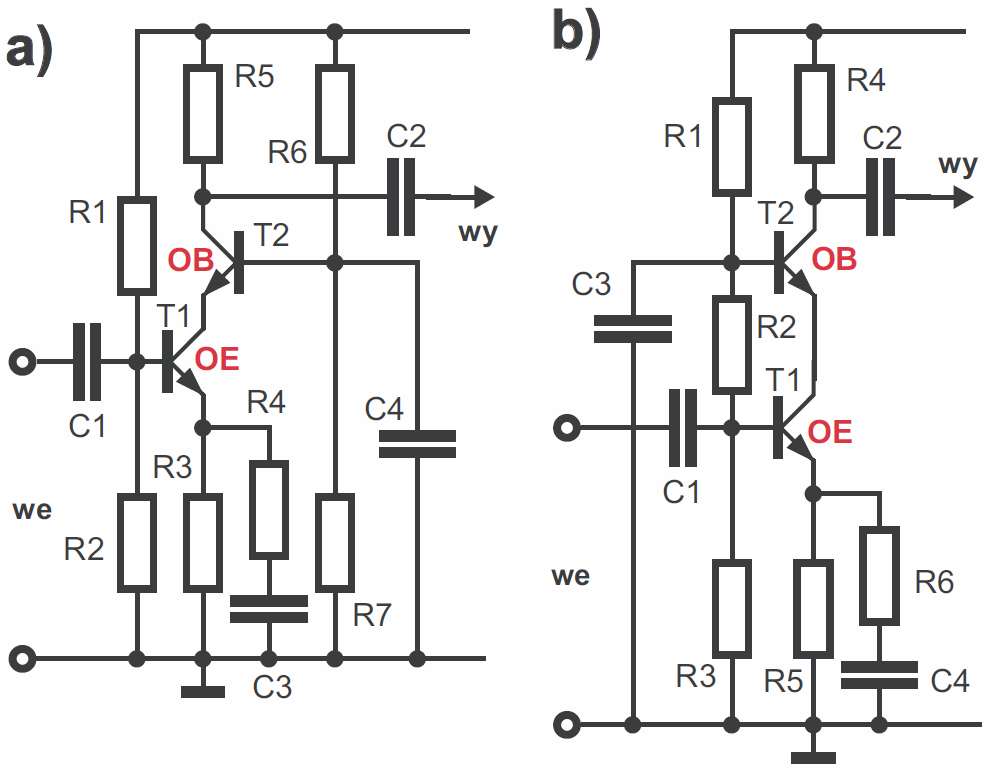
Inne konfiguracje. Połączenie układu OE i OB według rysunku 22 daje tak zwany wzmacniacz kaskodowy (nie mylić z kaskadowym), stosowany głównie w układach wysokonapięciowych oraz w urządzeniach wysokiej częstotliwości – radiowych. Tranzystor T1 pracuje w układzie OE, a T2 – OB.
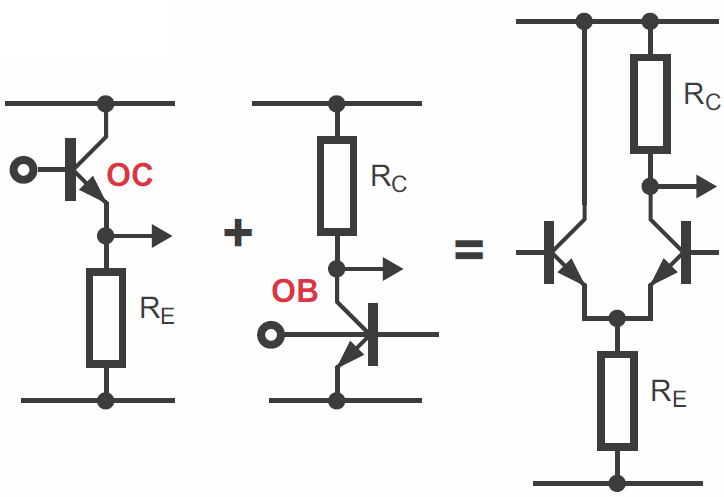
Natomiast połączenie układu OC z układem OB daje… znaną nam już parę różnicową z pojedynczym wyjściem – rysunek 23.
Problem oporności
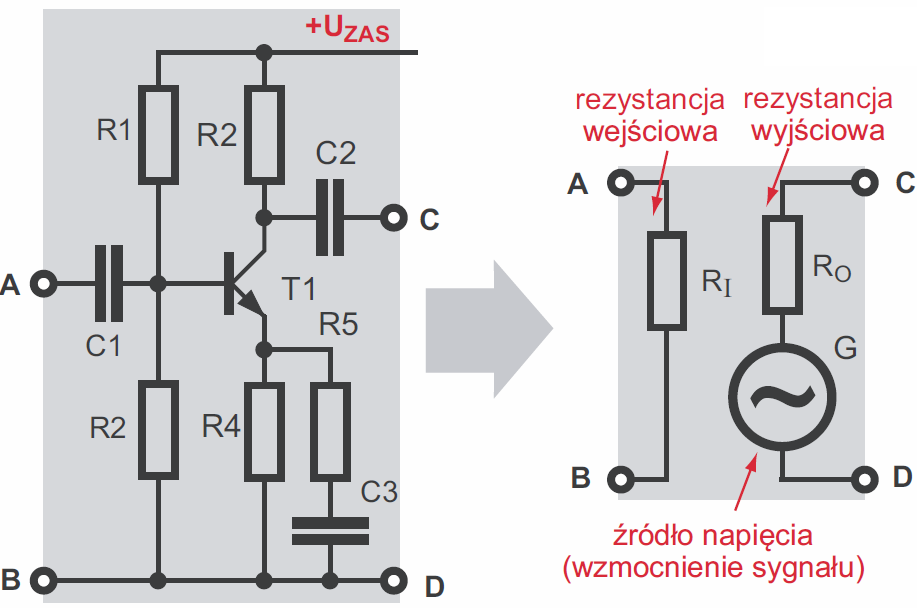
Często mówimy o oporności wejściowej czy wyjściowej. W baterii nie ma wewnątrz rezystora, a mówimy o rezystancji wewnętrznej (patrz wykład 8, rysunek 1). Takie podejście znakomicie ułatwia zrozumienie zachowania baterii „w kontaktach zewnętrznych” oraz obliczenia. Dokładnie tak samo jest z układami elektronicznymi. Często nie interesują nas wszystkie szczegóły, tylko zachowanie tego układu przy „kontaktach zewnętrznych”, co ułatwia obliczenia. Dlatego często traktujemy układ jak pełniącą dane funkcje „czarną skrzynkę” i interesuje nas tylko, jak zachowuje się wejście układu, a jak jego wyjście. Jeżeli jakiś układ ma wejście, to interesuje nas oporność tego wejścia (oporność widziana od strony wejścia). W przypadku wzmacniaczy, mikrofonów, generatorów, itp., zachowanie ich wyjść jest bardzo podobne do zachowania baterii. Schemat zastępczy wzmacniacza tranzystorowego dla przebiegów zmiennych można narysować jak na rysunku 24.
Rezystancje wejściowa RI oraz wyjściowa RO mają duże znaczenie np. przy łączeniu kaskadowym (nie kaskodowym) kilku stopni, jak ilustruje rysunek 25a, ponieważ rezystancja wejściowa obciąża wyjście poprzedniego stopnia. Tworzą się dzielniki, zmniejszające sygnał – rysunek 25b. Tylko w urządzeniach wysokiej częstotliwości (radiowych) rezystancja wyjściowa powinna być równa wejściowej, by uzyskać tak zwane dopasowanie falowe. Natomiast w pozostałych układach, w tym w urządzeniach audio, oporność (rezystancja) wyjściowa RO powinna być jak najmniejsza, a oporność wejściowa RI – jak największa.
Niestety różnie z bywa. Wtórnik, układ ze wspólnym kolektorem, ma dużą rezystancję wejściową i małą wyjściową, ale nie wzmacnia napięcia sygnału. Natomiast wzmacniacze OE, a tym bardziej OB mają stosunkowo małą rezystancję wejściową i stosunkowo dużą wyjściową.
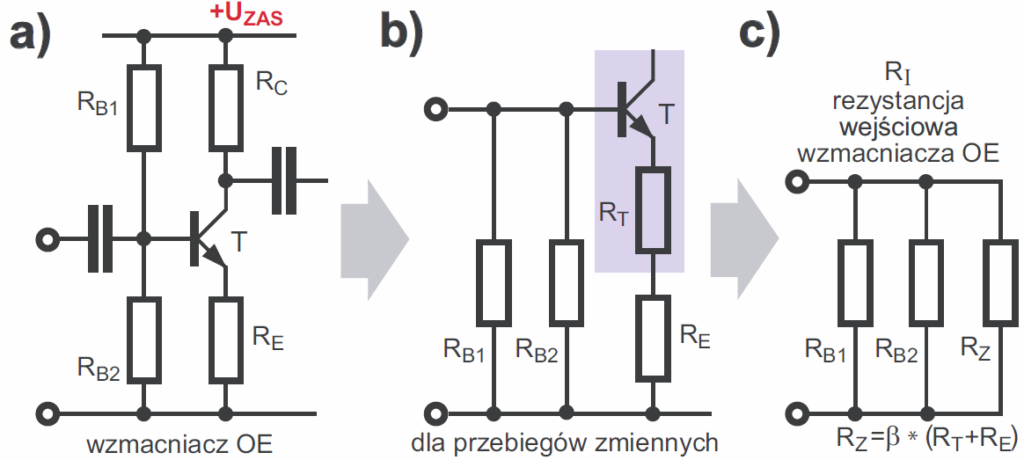
W układzie OE zwiększanie rezystancji emiterowej RE korzystnie zwiększa rezystancję wejściową – Jak pokazuje rysunek 26, rezystancja wejściowa samego tranzystora dla małych przebiegów zmiennych jest równa sumie rezystancji RT+RE pomnożonej przez wzmocnienie prądowe (w uproszczeniu β, ściślej przez małosygnałowe wzmocnienie zmiennoprądowe, oznaczane h21), ale do tego dochodzą dołączone równolegle rezystancje RB1, RB2. Dla przebiegów zmiennych wszystkie te rezystancje są połączone równolegle, co sygnalizował już rysunek 7c.
Jeszcze dziwniej jest z obwodem wyjściowym. Wcześniej cieszyliśmy się, że prąd kolektora nie zależy od napięcia na kolektorze i że obwód kolektora zachowuje się jak źródło prądowe. Z jednej strony to bardzo dobrze, ale jednocześnie oznacza to, że duże zmiany napięcia powodują znikome zmiany prądu, więc obwód kolektorowy tranzystora „sam z siebie” ma ogromną rezystancję wewnętrzną (dynamiczną). Dlatego we wzmacniaczach OE i OB rezystancja wyjściowa RO jest praktycznie równa wartości rezystora kolektorowego RC – rysunek 27.
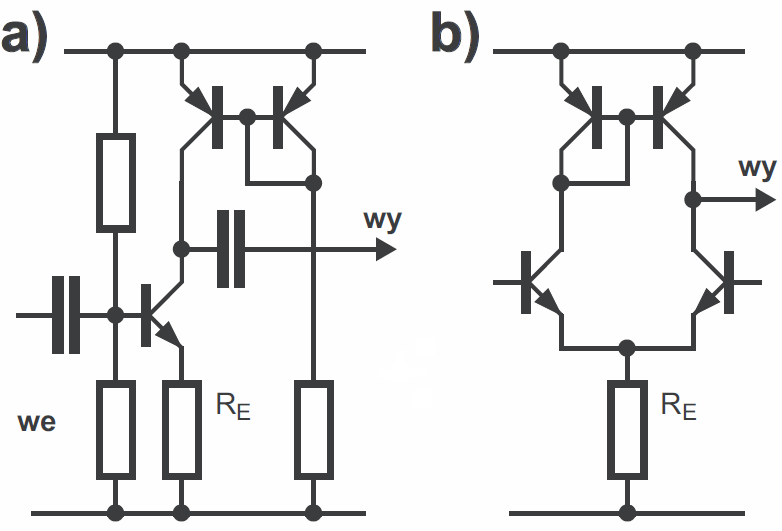
Jeśli chcemy uzyskać dużą wartość wzmocnienia napięciowego, to chcielibyśmy zastosować jak największą wartość RC (patrz wcześniejszy rysunek 15). Bardzo duże wzmocnienie napięciowe uzyskalibyśmy, włączając w kolektorze… źródło prądowe, które ma ogromną rezystancję dynamiczną, na przykład według rysunku 28a. W układach OE i OB tego nie robimy, ale ogromne wzmocnienie napięciowe możemy uzyskać w układzie pary różnicowej według rysunku 28b. Tego rodzaju wyjście ma jednak ogromną rezystancję wyjściową.
W praktyce problem likwidujemy, dodając wtórnik (układ OC), który z natury ma dużą rezystancję wejściową – przykłady na rysunku 29.
Sygnalizuję Ci tu w dużym skrócie bardzo ważne zagadnienia. Nie przejmuj się, jeśli na razie nie wszystko rozumiesz. Wystarczy, że zapamiętasz podstawowe informacje o prostych układach wzmacniających i z powodzeniem je zrealizujesz. A na zakończenie tego wykładu jeszcze pożyteczna propozycja układowa.
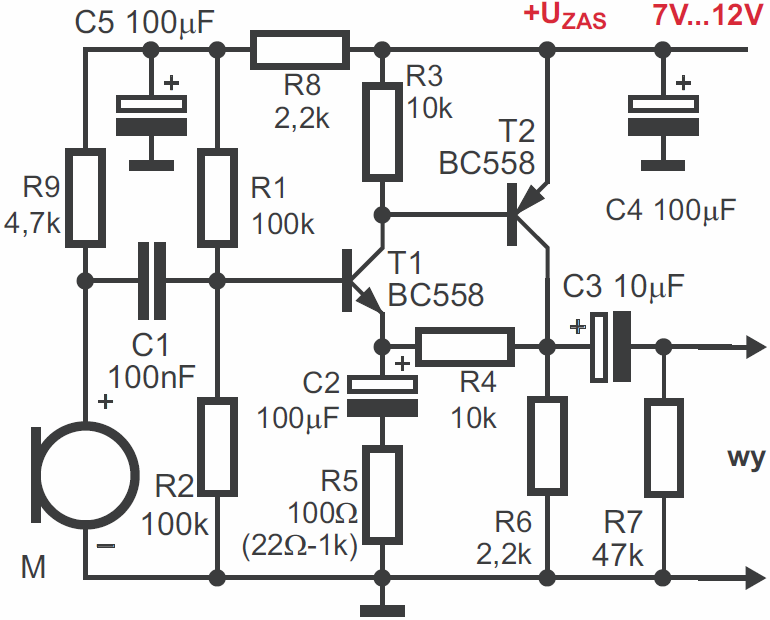
Przedwzmacniacz. Uniwersalny przedwzmacniacz dla małych sygnałów zmiennych (mikrofonowy) możesz zbudować według rysunku 30 i fotografii 31.
Taki przedwzmacniacz jest prostszy i ma parametry lepsze niż układy z rysunków 16 i 19, a to dzięki objęciu obu stopni wzmocnienia globalnym ujemnym sprzężeniem zwrotnym, które to sprzężenie, wbrew obiegowym opiniom, jest jak najbardziej pożyteczne. Bez ujemnego sprzężenia zwrotnego układ miałby ogromne wzmocnienie. Bardzo silne sprzężenie zwrotne dla prądu stałego i przebiegów wolnozmiennych realizuje rezystor R4 – dla takich sygnałów wzmocnienie byłoby równe jedności. Natomiast dla sygnałów akustycznych reaktancja pojemnościowa kondensatora C2 jest bardzo mała i dla takich sygnałów wzmocnienie wyznaczone jest przez stosunek rezystancji R4/R5. Aby ustawić wzmocnienie według potrzeb, należy dobrać wartość rezystora R5 w zakresie 22 Ω do 1 kΩ.
Piotr Górecki