Elektronika (nie tylko) dla informatyków (4) Potencjometry i …

W poprzednim wykładzie zaznajomiliśmy się z rezystorami precyzyjnymi. W tym odcinku skupimy się na potencjometrach oraz na coraz bardziej wykorzystywanych w teraźniejszej elektronice – rezystorach SMD.

Potencjometry i „peerki”

Problemy związane z precyzją dotyczą też rezystorów zmiennych, w szczególności różnego rodzaju potencjometrów. Choć potencjometry tracą swoje znaczenie w sprzęcie elektronicznym, będąc wypierane przez zaawansowane pokrętła i potencjometry elektroniczne, jednak nadal często używane są małe potencjometry montażowe, nazywane potocznie peerkami. Określenie „peerek” związane jest z tym, że potencjometry montażowe na schematach oznaczane są zwykle PR, w odróżnieniu od innych potencjometrów, oznaczanych zwykle literą P. Z kolei skrót PR pochodzi od preset resistor.

Tylko zupełnie początkujący uważają, że potencjometr montażowy to idealny sposób na uzyskanie rezystancji o dowolnej wartości. W praktyce bywa zupełnie inaczej. Owszem, w chwili regulacji ustawiona zostanie idealna wartość, ale wpływ temperatury, upływ czasu, wilgoć i kurz spowodują, że rezystancja popularnego peerka może zmienić się, i to bardzo poważnie.

Po pierwsze w zdecydowanej większości mamy do czynienia z potencjometrami węglowymi – fotografia 1. Materiałem czynnym ścieżki węglowej jest tam węgiel. Już to wskazuje, że właściwości nie są lepsze od rezystorów węglowych. Co gorsza, w takich potencjometrach substancja czynna nie jest chroniona przed wpływem czynników atmosferycznych. Starzenie może polegać na utlenianiu ścieżki węglowej albo reakcjach węgla z innymi substancjami zawartymi w powietrzu. Do tego dochodzi kurz i pył, który może osiadać na ścieżce oporowej. Oznacza to, że stabilność popularnych potencjometrów węglowych jest znacznie gorsza niż rezystorów węglowych. Cóż z tego, że ktoś ustawi potrzebną mu rezystancję, jeśli po pewnym czasie „rozjedzie się” ona o kilka, a w pewnych wypadkach nawet kilkanaście procent.

Trochę lepsze są potencjometry, w których ścieżka zbudowana jest z przewodzącego tworzywa sztucznego (plastic potentiometres). Znacznie lepsze są potencjometry cermetowe, zbudowane na bazie ceramiki i metalu.

Warto podkreślić, że potencjometry montażowe, czy to węglowe, czy cermetowe, mogą mieć budowę typu otwartego (open), gdzie ścieżka wystawiona jest na czynniki atmosferyczne. Są też typy zamknięte (housed), z różnymi rodzajami obudów chroniących przed kurzem. I trzecia grupa to potencjometry w obudowach szczelnych (sealed), chroniących nie tylko przed kurzem, ale też przed płynami używanymi w procesie automatycznego lutowania.

W urządzeniach pomiarowych często stosowane są obudowane potencjometry typu helitrim, gdzie suwak poruszany jest za pomocą śruby, co pozwala precyzyjnie ustawić rezystancję. Fotografia 2 pokazuje potencjometry cermetowe, zwykłe i helitrimy. Helitrimy, będące odmianą potencjometrów cermetowych, mają dobre parametry, porównywalne z rezystorami metalizowanymi. Przykładowo współczynnik cieplny TCR może wynosić 100 ppm/K lub nawet mniej.

Warto pamiętać, że potencjometry mają wartości według szeregu E3, obejmującego wartości 10, 22, 47, albo też pokrewnego 10, 20, 50 i że zwykle mają tolerancję 20%. Nie szukaj więc potencjometru 3,9 kΩ czy 75 kΩ – takich nie ma.

W praktyce często trzeba dobrać potencjometr i rezystor, żeby uzyskać potrzebny zakres zmian rezystancji. Można byłoby przeprowadzać ścisłe wyliczenia, uwzględniając tolerancje. Ale można to zrobić w sposób uproszczony.

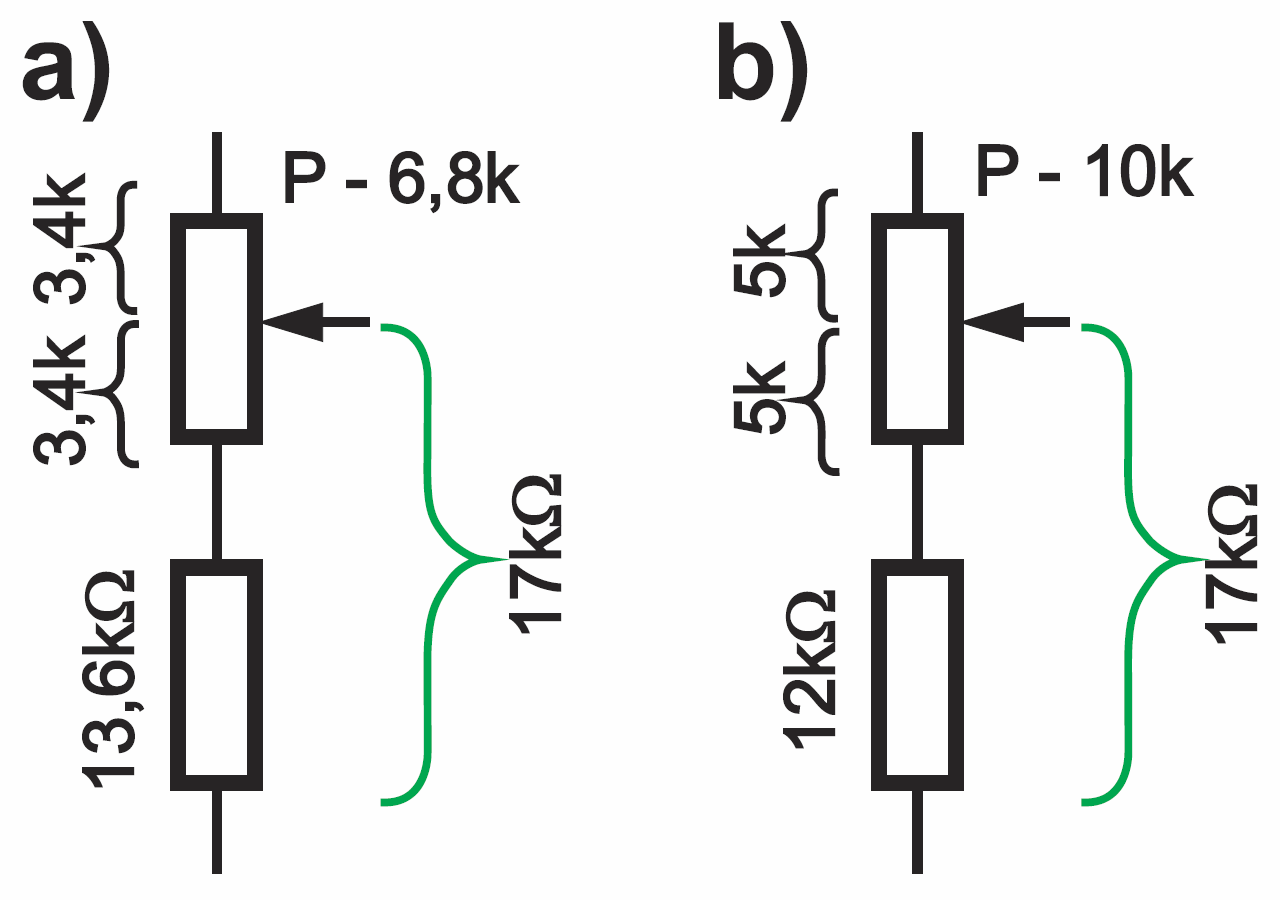
Na przykład z obliczeń wyszło nam, że wartość rezystancji ma wynosić 17 kΩ i że trzeba przewidzieć zakres regulacji ±20%, czyli ±3,4 kΩ. W środkowym położeniu suwaka potencjometru rezystancja powinna wynieść około 17 kΩ, a przesunięcie suwaka w skrajne położenie powinno zmienić rezystancję o 20%, czyli dać wartości 13,6 kΩ i 20,4 kΩ. Teoretycznie trzeba zastosować rezystor stały o wartości 13,6 kΩ i potencjometr o wartości 6,8 kΩ, jak wskazuje rysunek 3a. W praktyce potencjometru 6,8 kΩ nie da się kupić, więc choćby z tego względu trzeba zastosować potencjometr o bardzo popularnej wartości 10 kΩ ±20% i rezystor stały 12 kΩ ±5% według rysunku 3b. Da to też dodatkowy zapas regulacji.

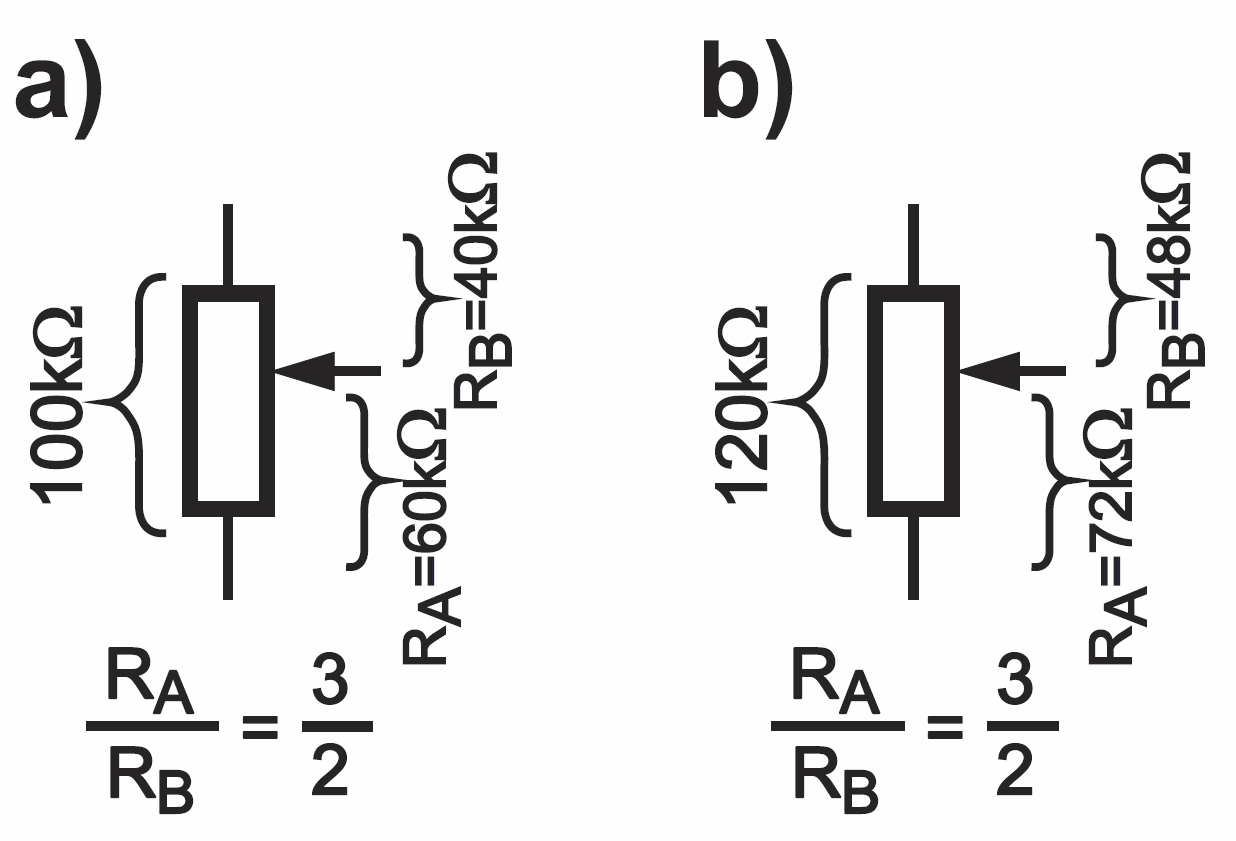
Choć w urządzeniach precyzyjnych powszechnie stosuje się potencjometry cermetowe, zwłaszcza wieloobrotowe helitrimy, warto pamiętać o kilku zależnościach umożliwiających zastosowanie „zwykłych peerków”. Mianowicie nawet jeśli rezystancja ścieżki potencjometru zmienia się np. pod wpływem temperatury, to niezmienny pozostaje (a przynajmniej powinien pozostać) współczynnik podziału dzielnika, co ilustruje w przesadzony sposób rysunek 4. Czyli w charakterze precyzyjnego dzielnika mógłby też pracować potencjometr o dużym współczynniku TCR.

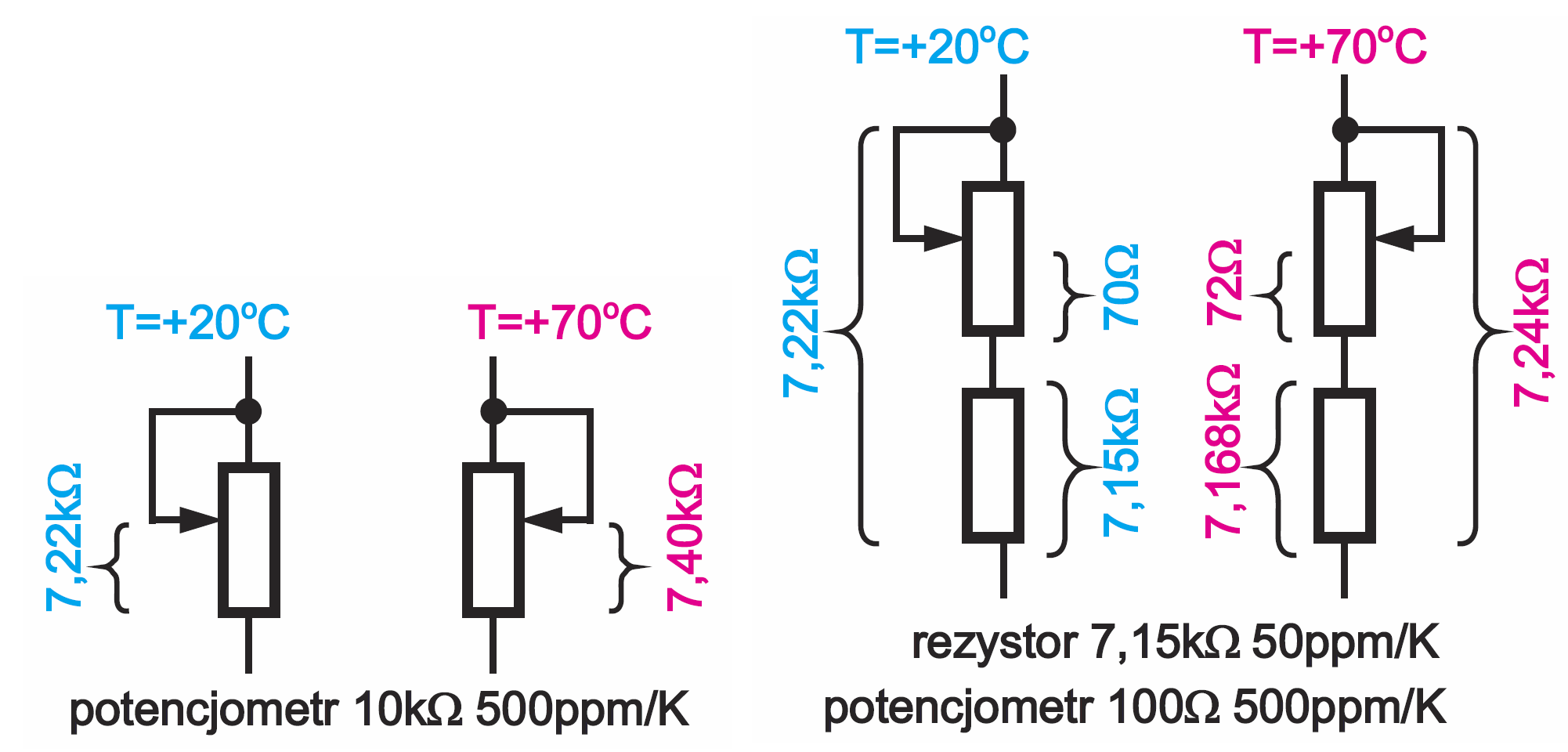
Druga sprawa to uzyskiwanie dokładnie określonej rezystancji za pomocą potencjometru. Teoretycznie można wykorzystać sam potencjometr, o ile uda się idealnie ustawić suwak. Ale znacznie lepiej jest włączyć w szereg dobrej jakości rezystor stały plus potencjometr o niewielkiej rezystancji. Rysunek 5 pokazuje przykład, o ile zmieni się rezystancja 7,22 kΩ przy wzroście temperatury z +20 °C do +70 °C w dwóch rozwiązaniach, jeśli zwykły potencjometr ma TCR = 500 ppm/K, a precyzyjny rezystor ma TCR = 50 ppm/K. Przy wzroście temperatury o 50 °C potencjometr zmieni rezystancję o 25000 ppm, czyli o 2,5%, natomiast rezystor tylko o 0,25%. Jak widać, w drugim przypadku nawet znacząca procentowa zmiana rezystancji potencjometru ma niewielki wpływ na rezystancję wypadkową z uwagi na małą rezystancję potencjometru.

Oznaczenia

Popularne rezystory najczęściej oznaczane są kodem barwnym, w którym o cyfrach i innych oznaczeniach informują kolorowe paski. Idea jest bardzo prosta: wartość wyrażona jest w omach.

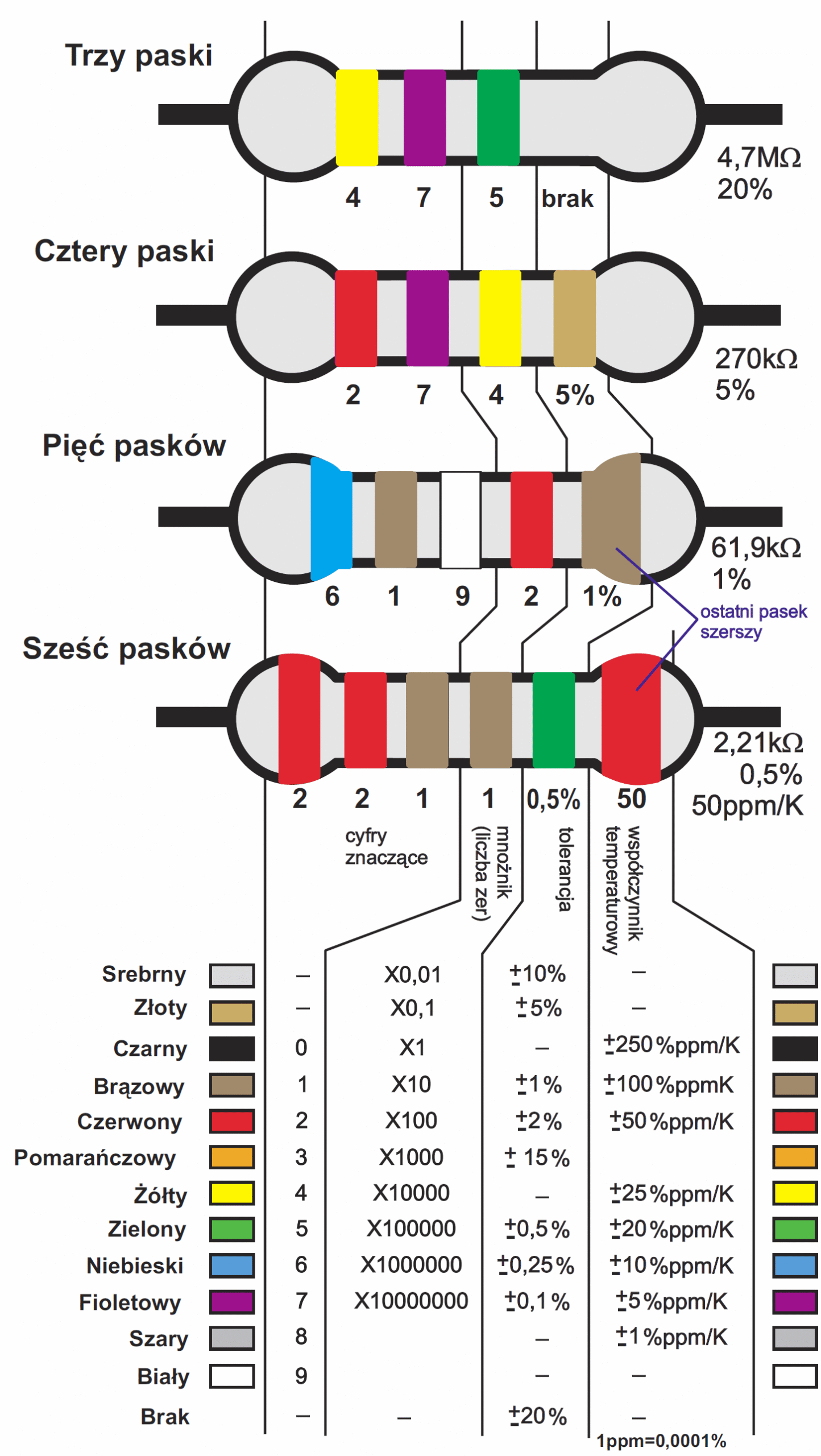
W przypadku rezystorów 5% o wartościach według szeregu E24 oznaczenie zawiera cztery paski. Dwa pierwsze zawsze określają nominał z szeregu E24, trzecia cyfra to mnożnik, a czwarta wskazuje tolerancję. Kluczem może być rysunek 6, pokazujący też kilka przykładów. Popularny, 5-procentowy rezystor ma cztery paski, z czego ostatni, wskazujący tolerancję, jest złoty. Jeśli paski są trzy, chodzi o stary rezystor o tolerancji 20%. Pięć lub sześć pasków wskazuje, że jest to rezystor precyzyjny.

Wcześniej wiele rezystorów miało oznaczenie cyfrowo-literowe. Zazwyczaj zamiast przecinka stosowano literę wskazującą mnożnik (k – kilo, M – mega, G – giga), przy czym w roli przecinka obok G, M, k, dodatkowo dla omów stosowano literkę R. Ewentualna czwarta litera wskazywała tolerancję według zasady: J – 5%, K – 10%, M – 20%.

I tak na przykład:

1R0 to 1,0 Ω    R33 to 0,33 Ω    56 lub 56R to 56 Ω    2M7J to 4,7 MΩ 5%    4R7K to 4,7 Ω 10%    2k2M to 2,2 kΩ 20%

Podobnie zapisane wartości (zwykle bez tolerancji) można też znaleźć na niektórych schematach. Fotografia 7 pokazuje kilka tak starych rezystorów oznaczonych cyframi.

Dziś w taki sposób oznacza się tylko rezystory dużej mocy – przykład zamieszczono na fotografii 8.

Oznaczenia rezystorów precyzyjnych

Łatwe do zdobycia rezystory o tolerancji 1% mają wartości nominalne według szeregu E96. Wtedy oznaczenie ma pięć pasków, a nie cztery. Pierwsze trzy określają nominał według szeregu E96, czwarty – mnożnik, a piąty tolerancję. Spotyka się też rezystory z sześcioma paskami, a wtedy ostatni oznacza współczynnik cieplny TCR. Kilka przykładów masz na fotografii 9 – zobacz też rysunek 6.

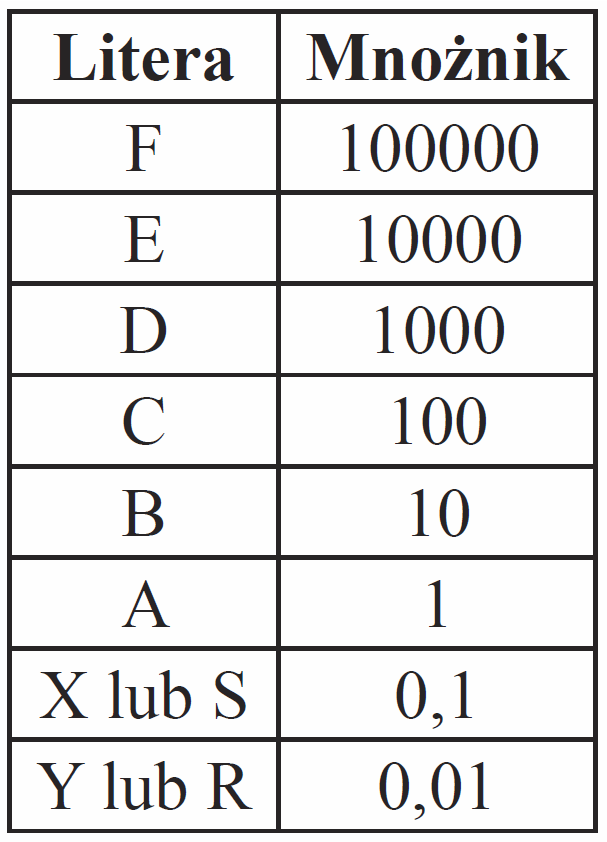
Spotyka się również rezystory precyzyjne oznaczone cyframi, a zamiast przecinka stosowane są litery R, k, M, G, określające mnożnik. Tolerancja oznaczona jest literą. Oprócz wcześniej poznanych J, K, M oznaczających tolerancję odpowiednio 5%, 10%, 20%, stosowane są też inne litery wg tabeli 10.

Zasadniczo rezystory precyzyjne mają nominały według szeregu E96 lub półprocentowego E192. Ale co ciekawe, niektóre firmy produkują też jednoprocentowe rezystory o nominałach z szeregu E24 – przykład pokazany jest na fotografii 11.

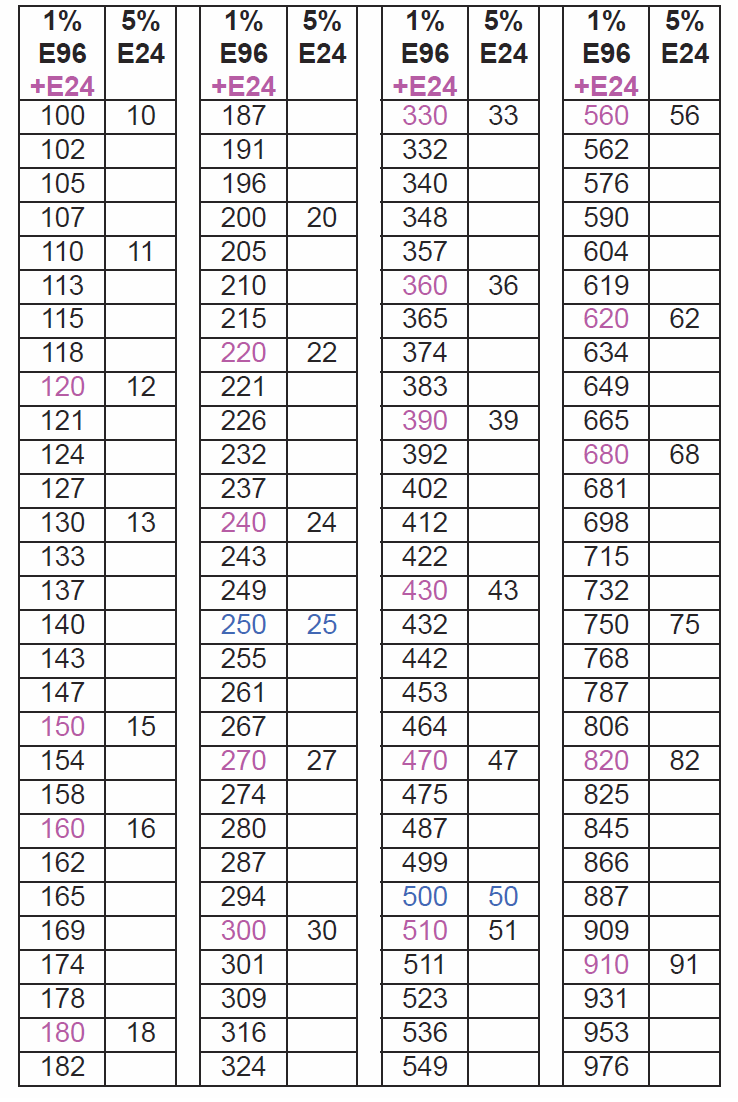
W tabeli 12 podane są wartości wzbogaconego szeregu E96 + E24 z zaznaczonymi na niebiesko trzema dodatkowymi wartościami z nietypowego szeregu E3.

Rezystory SMD

W dobie gwałtownej miniaturyzacji wykorzystuje się coraz mniejsze rezystory. Do dziś dostępne są rezystory MELF, które można uważać za miniaturowe wersje klasycznych rezystorów, tylko bez końcówek z drutu – patrz fotografia 13. Są one lutowane wprost do pól lutowniczych, czyli są elementami do montażu powierzchniowego – SMD.

Dziś zdecydowana większość rezystorów SMD to kostki (chip resistors) o różnej wielkości – patrz fotografia 14.

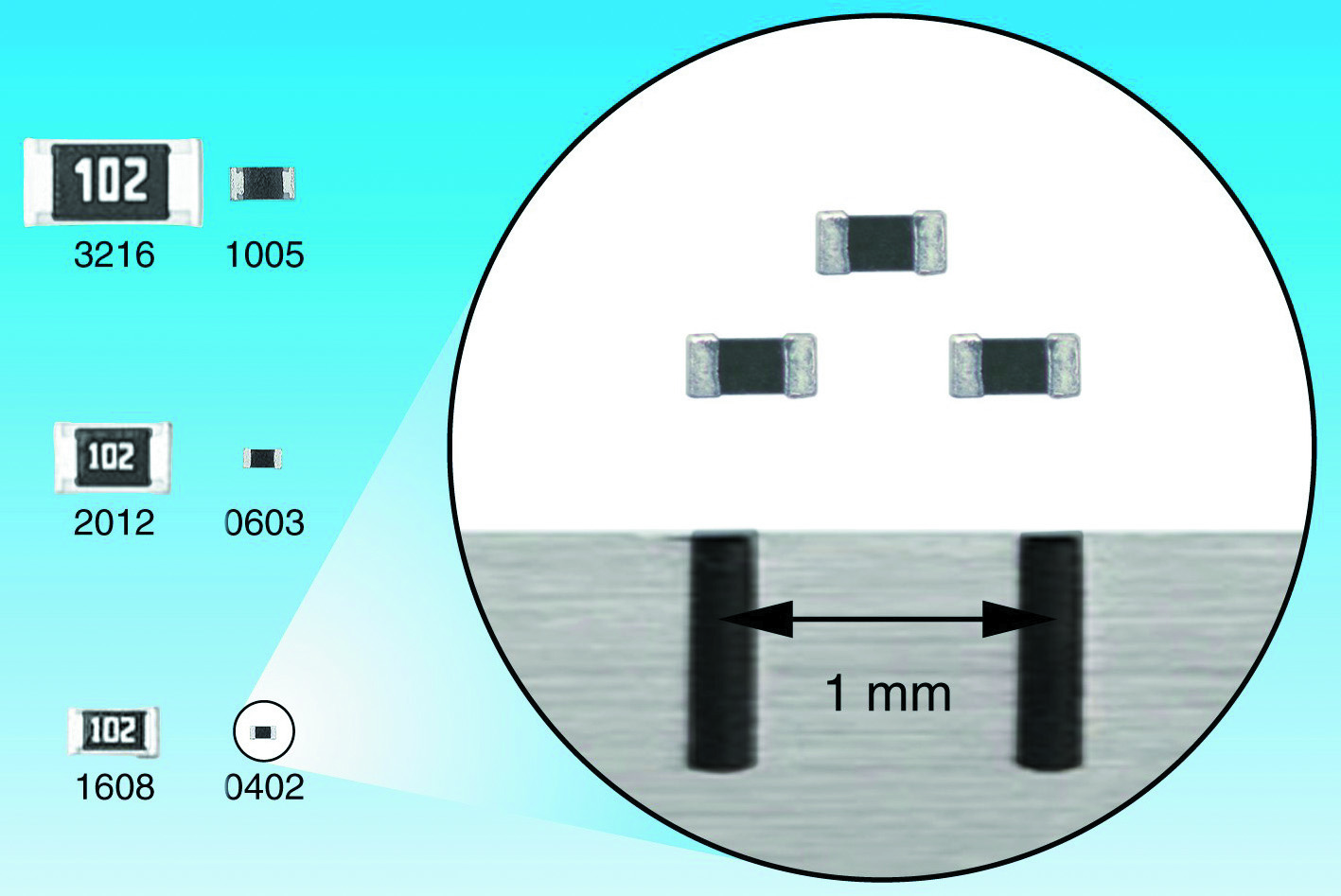
Rozmiary elementów SMD podaje się zazwyczaj w postaci czterech cyfr, na przykład 1206, 0603, 0805 czy 0402. Są to dwie dwucyfrowe liczby określające długość i szerokość w dziesiątkach milsów. Jeśli jeszcze nie wiesz, co to jest mils, to zapamiętaj, że jest to jedna tysięczna cala. Stąd 10 milsów to 10 × 1/1000 × 25,4 mm czyli 0,254 mm. W przybliżeniu możesz spokojnie przyjąć, że 10 milsów to ćwierć milimetra. Tym samym element wielkości 1206 ma wymiary 12×0,25 mm = 3 mm na 6×0,25 mm = 1,5 mm. Dziś typowo stosowane rezystory i inne elementy SMD mają wielkość 0603 czyli 1,5 mm × 0,75 mm oraz 0402, czyli 1 mm × 0,5 mm. Fotografia 15 (Panasonic) ilustruje skalę miniaturyzacji. Co ciekawe, dziś dostępne są jeszcze mniejsze elementy o rozmiarach 0201 (0,6 mm × 0,3 mm), a także 01005 (0,4 mm × 0,2 mm). Nietrudno się domyślić, że obciążalność takich maleństw, a także maksymalne napięcie pracy, są bardzo małe. Przykładowo rezystory o wielkości 01005 mogą mieć obciążalność rzędu 30 mW i napięcie maksymalne 15 V, a wielkości 2512 – nawet do 2 W i napięcie do kilkuset woltów.

Rezystory SMD o większych rozmiarach są oznakowane, a na tych najmniejszych napisów nie ma. „Zwykłe” 5-procentowe rezystory SMD oznaczane są trzema cyframi – dwie pierwsze cyfry to nominał z szeregu E24, trzecia cyfra to mnożnik – patrz fotografia 16.

W razie potrzeby rolę przecinka pełni litera R. Oto kilka przykładów:
225 oznacza 2,2 MΩ   221 oznacza 220 Ω   220 oznacza 22 Ω   2R2 oznacza 2,2 Ω   R22 oznacza 0,22 Ω

Warto nadmienić, że dość często spotyka się miniaturowe rezystory SMD oznaczone 000 – fotografia 17. W istocie są to najzwyczajniejsze zwory o jak najmniejszej rezystancji i są stosowane np. wtedy, gdy projektant płytki ma kłopot z poprowadzeniem ścieżek na płytce drukowanej.

Ale dostępne są też rezystory SMD o bardzo małej rezystancji, rzędu nawet pojedynczych miliomów. Litera R pełni rolę przecinka i wskazuje, że rezystancja podana jest w omach. Rolę przecinka może pełnić też litera L, ale wtedy rezystancja podana jest w miliomach (1 mΩ = 0,001 Ω) – patrz fotografia 18. Spotyka się też oznaczenia rezystorów niskoomowych bez liter, a za to trzycyfrowe oznaczenie jest podkreślone. I tak na przykład zarówno R022, 022, jak i 22L oznaczają rezystancję 0,022 Ω, czyli 22 mΩ. Rezystancja takich oporników może być nawet mniejsza niż „zwór” 000, ale jest ściśle określona i takie rezystory zazwyczaj pracują w roli czujników prądu (mierzony jest spadek napięcia na nich).

Precyzyjne 1-procentowe rezystory SMD oznaczane są zwykle czterema cyframi, z których trzy określają nominał według szeregu E96, a czwarta to mnożnik – patrz fotografia 19.

 

 

 

Oto przykłady:

2213 oznacza 221 kΩ

2212 oznacza 22,1 kΩ

2211 oznacza 2,21 kΩ

2210 oznacza 221 Ω

22R1 oznacza 22,1 Ω

2R21 oznacza 2,2 Ω

R221 oznacza 0,22 Ω

R020 oznacza 0,020 Ω

 

 

 

 

 

 

Od pewnego czasu spotyka się też rezystory SMD kodowane inaczej (tzw. kod EIA-96), za pomocą dwóch cyfr i litery. Litera zawsze określa mnożnik – patrz tabela 20.

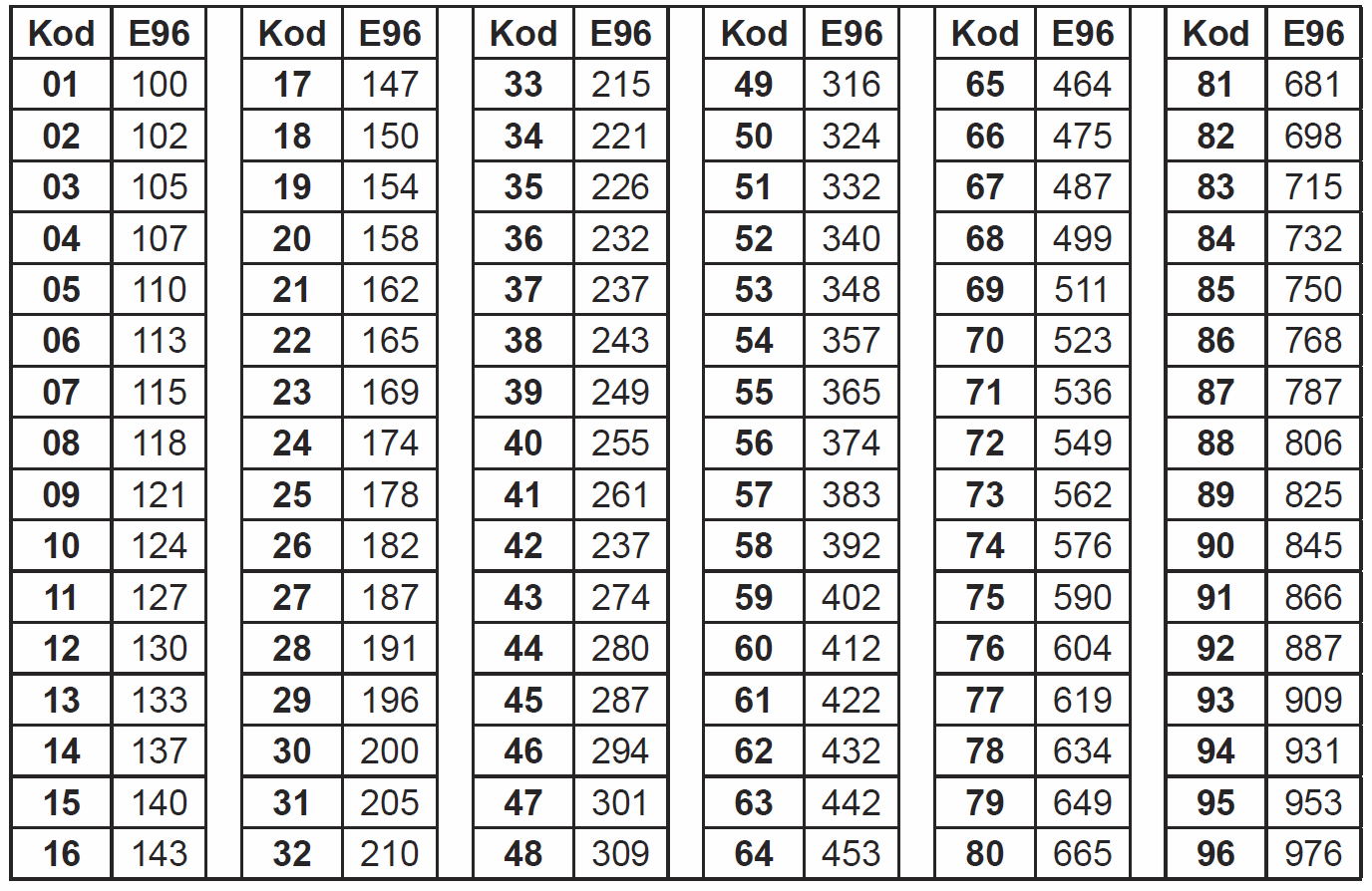
Ważna jest kolejność. Jeśli litera jest na końcu, to chodzi o rezystor o tolerancji 1% i dwie pierwsze cyfry kodu 01…96 określają numer kolejny nominału według szeregu E96 zgodnie z tabelą 21.

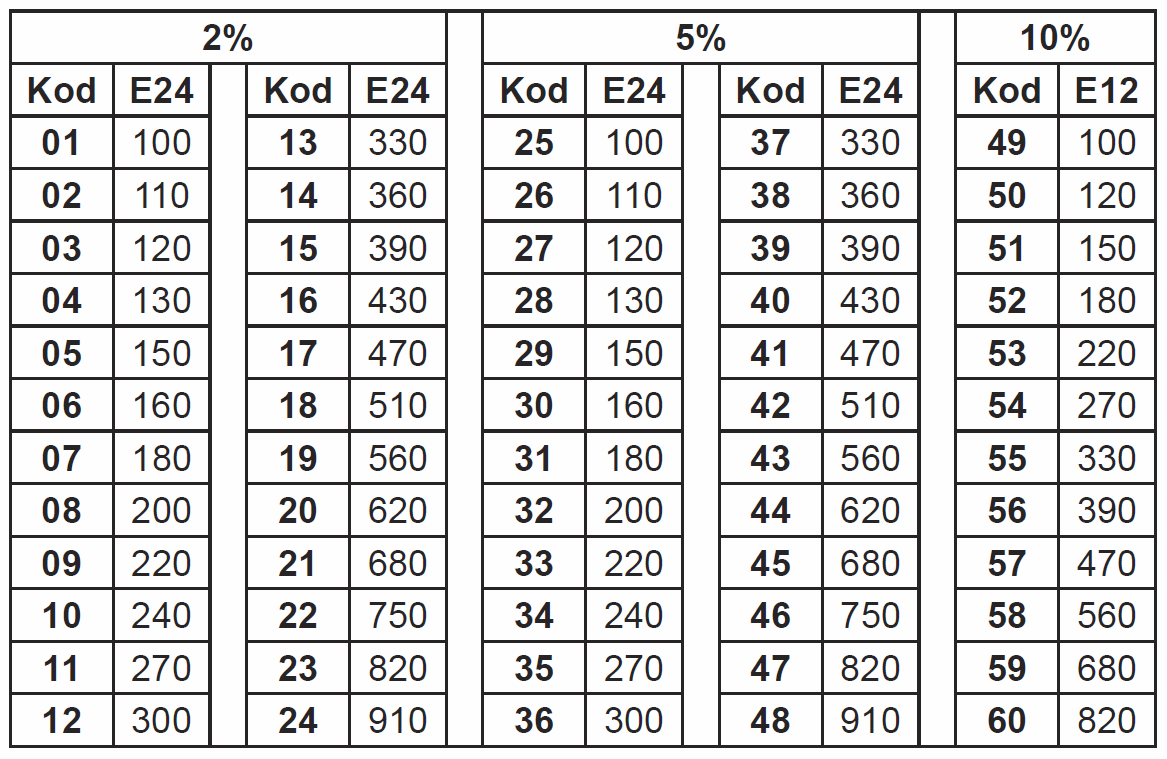
Natomiast jeśli litera jest pierwszym znakiem, wtedy chodzi o element o tolerancji 2%, 5% lub 10%. Za literą wystąpi liczba dwucyfrowa, która określa nie tylko nominał, ale też od razu tolerancję – patrz tabela 22.

Kilka przykładów:

22A – 165 × 1 = 165 Ω 1%   68C – 499 × 100 = 49,9 kΩ 1%    43E – 274 × 10000 = 2,74 MΩ 1%   A44 – 620 × 1 = 620 Ω 5%
D59 – 680 × 1000 = 680 kΩ 10%   B05 – 150 × 10 = 1,5 kΩ 2%   B29 – 150 × 10 = 1,5 kΩ 5%   B51 – 150 × 10 = 1,5 kΩ 10%

Oczywiście zawsze oporność rezystora można skontrolować omomierzem.

A w kolejnym odcinku zajmiemy się kondensatorami.

Piotr Górecki