Elektronika (nie tylko) dla informatyków (33) Niedoskonałość kondensatorów

W poprzednim odcinku spróbowaliśmy narysować w miarę kompletny schemat zastępczy rzeczywistego transformatora dla różnych częstotliwości pracy. W tym odcinku wracamy do kondensatorów, omówimy zagadnienia związane z niedoskonalością tych elementów.

Rzeczywisty kondensator

Idealny kondensator ma tylko jeden parametr – pojemność elektryczną C. W rzeczywistych kondensatorach drugim podstawowym parametrem jest napięcie maksymalne. Otóż przy zbyt wysokim napięciu kondensator, a ściślej jego dielektryk, zostanie uszkodzony – przebity. Przebicie może spowodować zwarcie okładek – kondensator stanie się wtedy zworą, rezystorem o znikomej wartości.

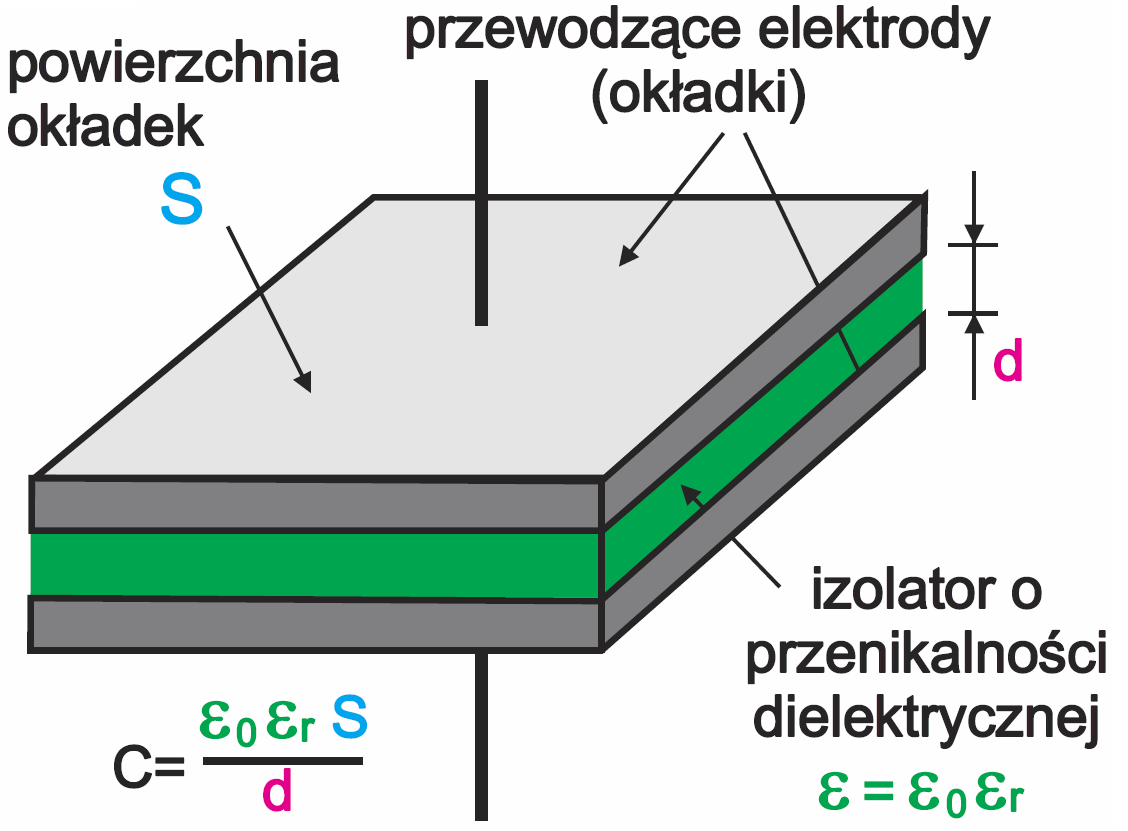
W sumie prawie wszystko zależy tu od dielektryka, czyli izolatora. Jak wskazuje rysunek 1 i podręcznikowy wzór:

C = ε S / d = ε_r ε₀ S / d

Pojemność C zależy od powierzchni okładek S, od grubości dielektryka d, a także od właściwości materiału dielektryka, a konkretnie od jego przenikalności elektrycznej ε. I tu znów widzimy pewien aspekt podobieństwa cewek i kondensatorów. Przy omawianiu właściwości rdzeni w transformatorach i cewkach stwierdziliśmy, że m.in. rdzenie charakteryzują się określoną przenikalnością magnetyczną μ, która jest iloczynem przenikalności magnetycznej próżni μ₀ i przenikalności względnej μ_r. W przypadku kondensatorów jest bardzo podobnie. Tu też ogromne znaczenie ma „rdzeń kondensatora”, czyli jego dielektryk. Całkowitą przenikalność elektryczną ε dielektryka określamy jako iloczyn przenikalności próżni ε₀ i przenikalności względnej ε_r.

Nie będziemy wchodzić we wszystkie szczegóły, ale przypomnijmy, że indukcyjność L cewki zależy od przenikalności magnetycznej μ_r jej rdzenia. Tak samo pojemność kondensatora C zależy od przenikalności elektrycznej ε_r „rdzenia”, czyli dielektryka. W przypadku transformatora zależało nam na jak największej przenikalności rdzenia. Dokładnie tak samo jest w przypadku kondensatorów: jeżeli chcemy uzyskać dużą pojemność, powinniśmy wykorzystać dielektryk o jak największej przenikalności ε_r. I tu znów występuje podobieństwo do materiałów magnetycznych: w zdecydowanej większości materiałów przenikalność magnetyczna μ_r jest mała, a bardzo duże wartości μ_r mają tylko materiały ferromagnetyczne, jednak niestety ich przenikalność nie jest stała, tylko jest nieliniowa, bo zależy od natężenia pola H i indukcji B, a w sumie od prądu. Na dodatek występuje tam histereza. Dla wielu zaskoczeniem będzie informacja, że dokładnie tak samo jest w kondensatorach. O ile większość materiałów ma niewielką względną przenikalność elektryczną ε_r w zakresie od 1 do co najwyżej kilkudziesięciu, o tyle istnieją też materiały, które mają bardzo dużą wartość przenikalności ε_r, powyżej 1000.

Jak się słusznie domyślasz, materiały te nazywane są ferroelektrykami i podobnie jak w ferromagnetykach duża przenikalność związana jest z nieliniowością charakterystyki oraz z występowaniem histerezy. W ferroelektrykach też występuje spontaniczna elektryzacja w postaci domen, a jednym z istotnych parametrów jest temperatura Curie, powyżej której ferroelektryk drastycznie zmniejsza swą przenikalność i staje się paraelektrykiem.

Materiały ferroelektryczne, w postaci specjalnych odmian ceramiki, wykorzystywane są do budowy niektórych kondensatorów, a konkretnie ceramicznych kondensatorów ferroelektrycznych. Ich pojemność przy małych rozmiarach jest zaskakująco duża. Niestety, jest to okupione m.in. nieliniowością i histerezą. A nieliniowość oznacza, że pojemność kondensatora ferroelektrycznego nie jest stała, tylko zależna od aktualnego napięcia panującego na kondensatorze. Ponieważ przenikalność ferroelektryków zmniejsza się ze wzrostem częstotliwości, maleje wtedy pojemność. Przenikalność ferroelektryków silnie zależy też od temperatury. Ze względu na występowanie histerezy pojawiają się też straty. Podkreślam, że mówimy teraz o kondensatorach ceramicznych z dielektrykiem ferroelektrycznym. Podobnie złe niektóre właściwości mają popularne kondensatory elektrolityczne. Zastosowany w nich dielektryk ma wprawdzie bardzo dobre właściwości, ale występują tam inne problemy, związane ze specyficzną budową. Kondensatory elektrolityczne mają duże pojemności, ale nadają się do pracy tylko przy stosunkowo małych częstotliwościach – przy wyższych szybko tracą pojemność i występują w nich duże straty. Natomiast jeszcze inne kondensatory, w tym ceramiczne, ale z innym dielektrykiem (nie ferroelektryczne) nie mają opisanych wad. Niektóre kondensatory ze zwykłej ceramiki mają bardzo dobrą stabilność cieplną, napięciową, znakomitą liniowość i znikome straty.

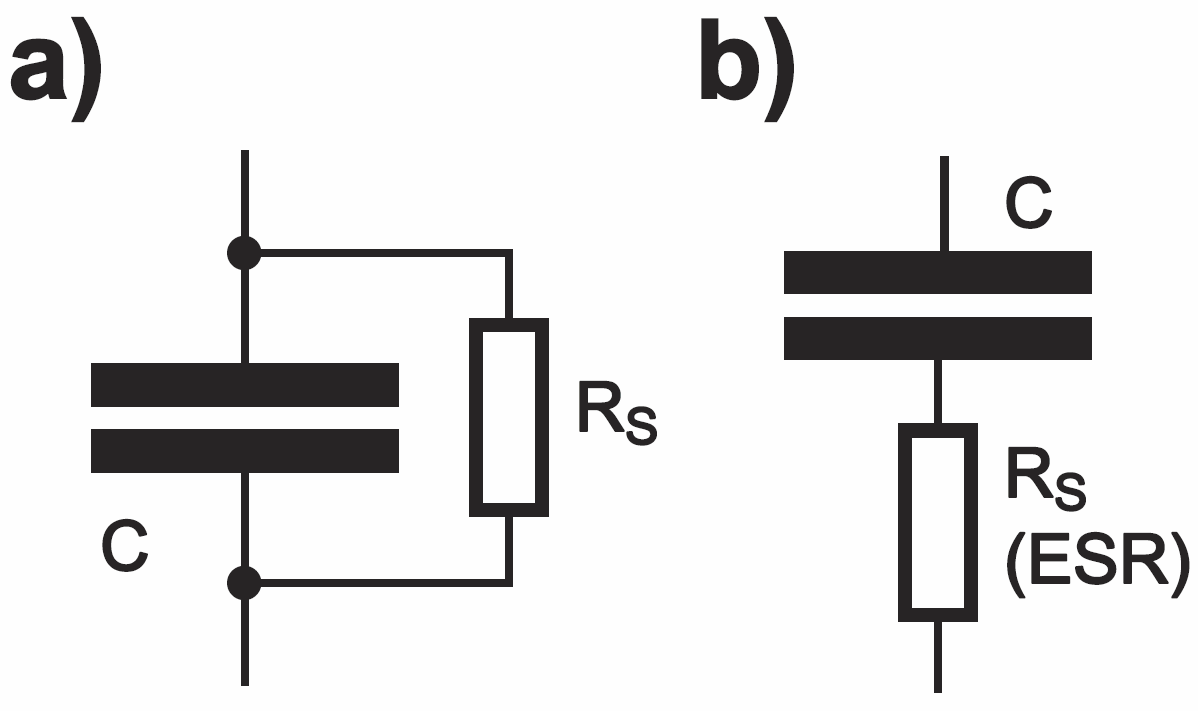
Trudno w prosty i przejrzysty sposób opisać wszystkie właściwości kondensatora i zależność pojemności C od temperatury, napięcia, częstotliwości. Prawie wszystko zależy od właściwości dielektryka. Straty w dielektryku, związane z cyklicznym elektryzowaniem, można przedstawić na schemacie zastępczym w postaci rezystancji (której wartość będzie jednak zależna od kilku czynników). Taką rezystancję można na schemacie zastępczym włączyć równolegle do pojemności C, jak pokazuje rysunek 2a. I tu początkującym wydaje się, że taka rezystancja będzie też oznaczać, że przez kondensator będzie płynął prąd stały, tak zwany prąd upływu. Jest to błędne wyobrażenie. Owszem, w nielicznych rodzajach kondensatorów, np. w elektrolitycznych, może wystąpić niewielki prąd upływu – prąd stały. Ale w zdecydowanej większości kondensatorów prąd upływu jest tak znikomo mały, że spokojnie można o nim zapomnieć. Rezystancja z rysunku 2a nie ma żadnego związku z prądem stałym – reprezentuje straty w dielektryku występujące przy przebiegach zmiennych. Niemniej dla uniknięcia wątpliwości, można i warto rezystancję reprezentującą straty narysować jak na rysunku 2b. Taka zastępcza szeregowa rezystancja strat jest często nazywana i oznaczana ESR (Equivalent Series Resistance). W niektórych zastosowaniach jest to bardzo ważny, wręcz krytyczny parametr kondensatora.

W kondensatorze nie ma wbudowanego wewnętrznego rezystora, ale taka reprezentacja strat jest zgodna z intuicją: podczas pracy przez kondensator płynie prąd zmienny i prąd ten, płynąc przez rezystancję ESR powoduje wydzielanie się ciepła – mocy strat P=I²R. Ciepło to skutkuje wzrostem temperatury, pogorszeniem parametrów, w tym niezawodności i trwałości. A przy nadmiernym wzroście temperatury skutkuje też bezpowrotnym uszkodzeniem kondensatora. Problem ten najostrzej występuje w kondensatorach, które pracują w indukcyjnych przetwornicach impulsowych i w nadajnikach w.cz. dużej mocy.

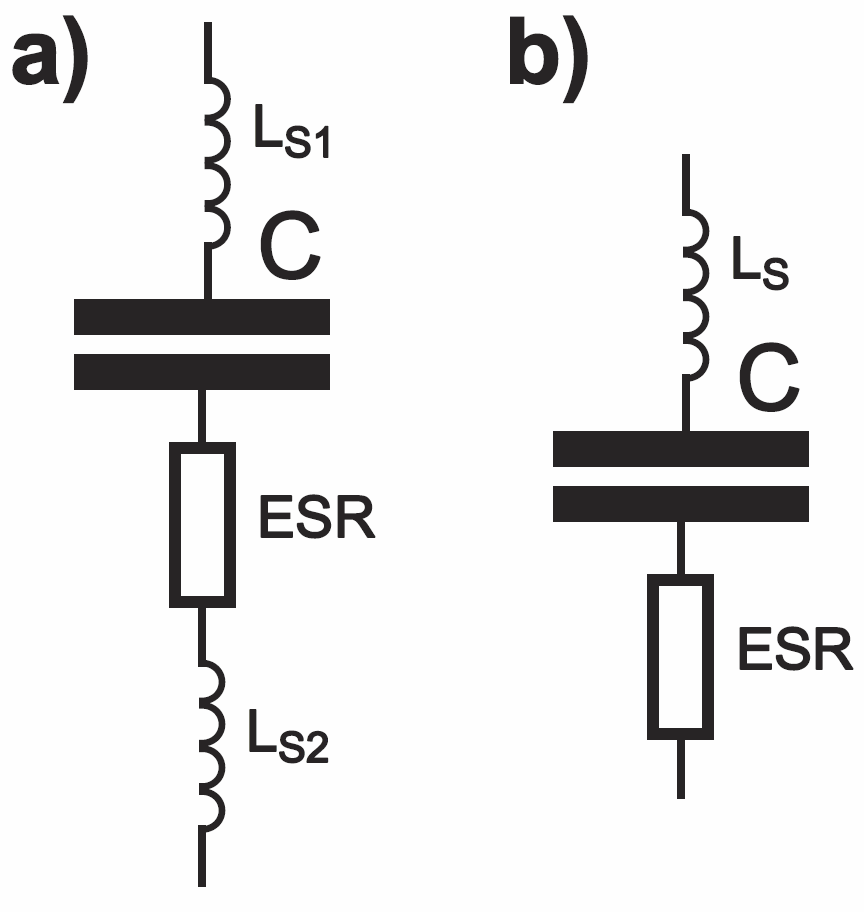
Ale ściślej biorąc, oprócz szeregowej rezystancji strat ESR, w kondensatorze mamy też inne szkodliwe czynniki. Na przykład drutowe wyprowadzenia (końcówki), a w niektórych kondensatorach także sposób ukształtowania elektrod, stanową pewną niewielką indukcyjność, co można zaznaczyć jak na rysunku 3.

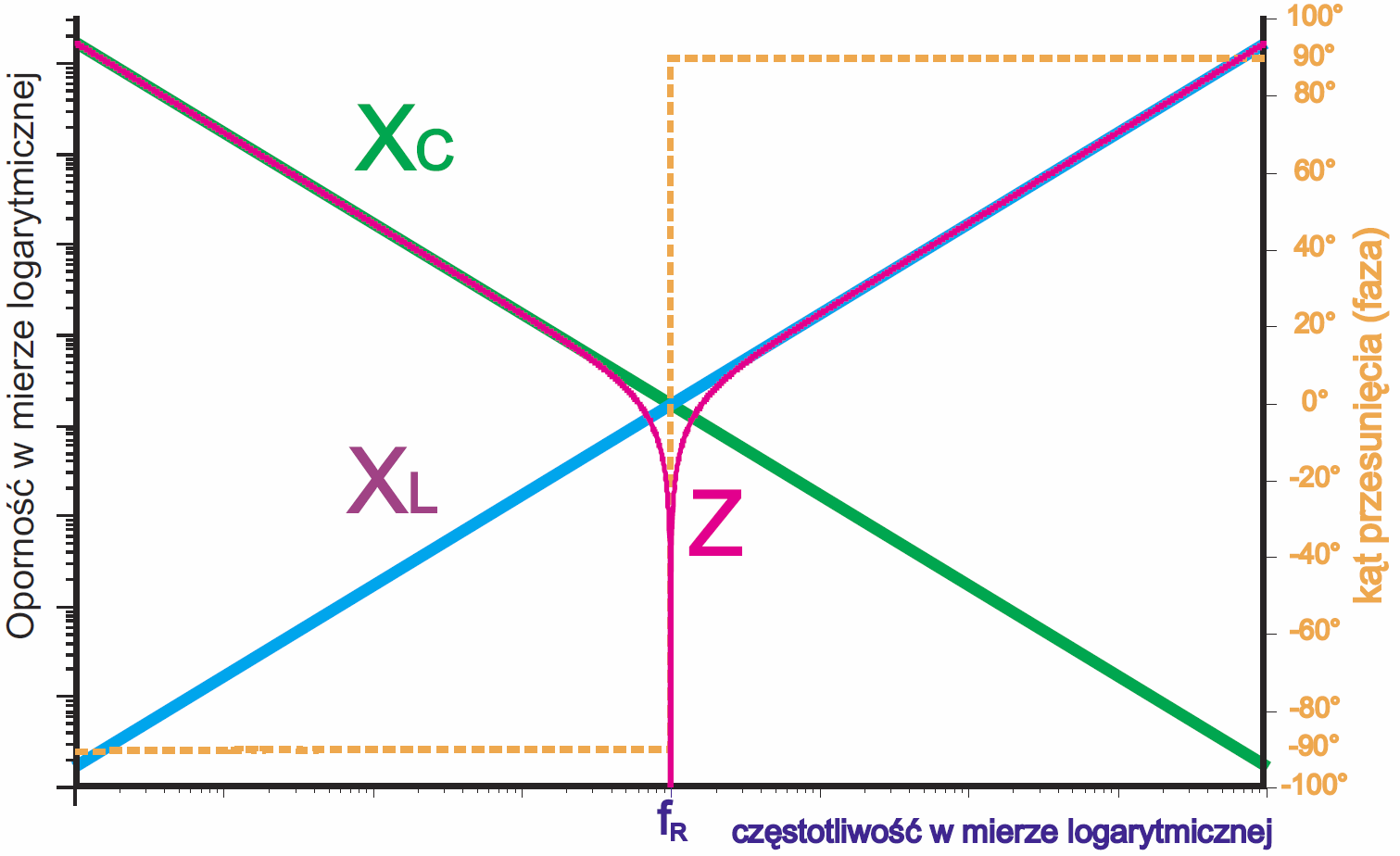
Przy mniejszych częstotliwościach można pominąć wpływ tej pasożytniczej indukcyjności L_S, ale przy wyższych częstotliwościach pojawia się problem. Otóż wiadomo, że kondensator dla prądów zmiennych stanowi pewną oporność – reaktancję pojemnościową X_C: X_C= 1 / 2πfC i że w kondensatorze napięcie opóźnia się względem prądu o ćwierć okresu (o kąt 90 stopni). Tymczasem okazuje się, że kondensator zachowuje się jak szeregowy obwód rezonansowy. Rysunek 4 pokazuje idealny przypadek – reaktancję szeregowego połączenia LC.

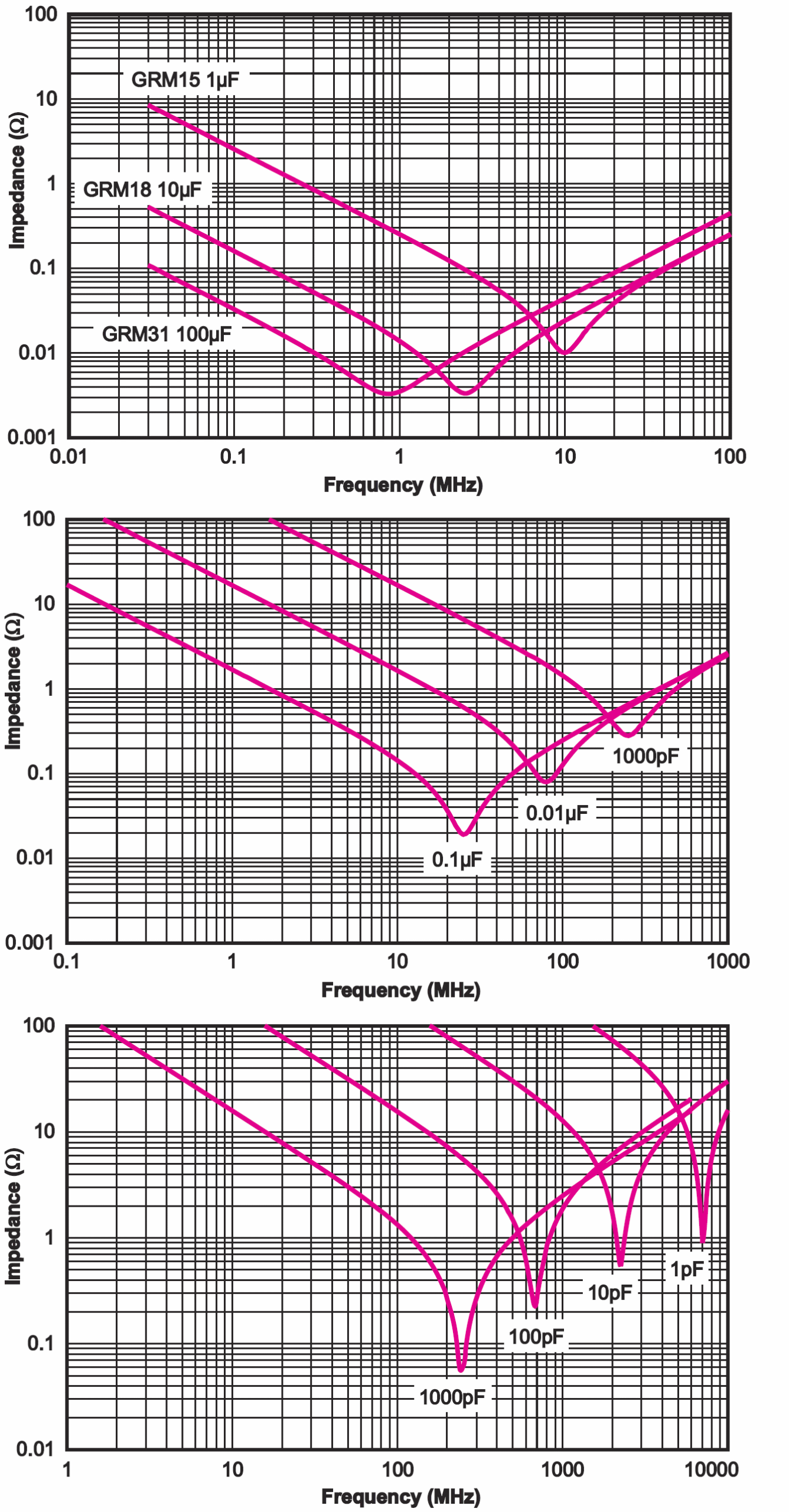
Owszem, dla mniejszych częstotliwości kondensator zachowuje się prawidłowo, jak kondensator idealny. Zielona prosta pokazuje, że reaktancja pojemnościowa maleje ze wzrostem częstotliwości. Reaktancja kondensatora, zaznaczona linią czerwoną, maleje i przesunięcie fazy (linia żółta) jest charakterystyczne dla kondensatora. Jednak przy wyższych częstotliwościach daje o sobie znać pasożytnicza reaktancja indukcyjna X_L. Dla jakiejś częstotliwości f_R następuje rezonans szeregowy i reaktancja dąży do zera. W praktycznym kondensatorze występuje jeszcze rezystancja strat, dlatego wypadkowa oporność – impedancja przy tej częstotliwości rezonansowej staje się równa ESR, a dokładniej biorąc… przy częstotliwości f_R kondensator staje się rezystorem o niewielkiej rezystancji ESR. Przy częstotliwościach wyższych od f_R dominuje coraz większa reaktancja indukcyjna i kondensator przy wysokich częstotliwościach zachowuje się… jak cewka i wtedy prąd opóźnia się względem napięcia, jak w każdej indukcyjności. Większość kondensatorów zachowuje się właśnie w taki sposób, jak szeregowe obwody rezonansowe i czym większa pojemność, tym niższa częstotliwość rezonansowa, jak pokazuje rysunek 5, pochodzący z katalogu kondensatorów ceramicznych firmy MuRata. Jak widać, ze wzrostem częstotliwości znacząco rosną też straty, czyli rośnie zastępcza rezystancja szeregowa ESR.

Jak z tego widać, na pozór prosty kondensator też kryje w sobie sporo tajemnic. Podobnie jest z rezystorem, uważanym za najprostszy, prymitywny element elektroniczny. Zajmiemy się tym w następnym odcinku.

Piotr Górecki