Zrozumieć mikroprocesory – jednostka ALU

Naturalnym jest, że mikroprocesor potrafi realizować operacje arytmetyczne. Kolejna część cyklu poświęcona jest jednostce arytmetyczno-logicznej. To taki element w każdym mikroprocesorze odpowiedzialny za obliczenia. Jak on to robi?Każdy mikroprocesor potrafi wykonać proste działania logiczne oraz arytmetyczne. Tymi działaniami zajmuje się ALU (ang. Arithmetic Logic Unit) – jednostka arytmetyczno-logiczna. Realizacja tych pierwszych (logicznych) jest banalnie prosta. Te drugie (arytmetyczne) to już inny, szerszy temat, przede wszystkim ze względu na liczbę możliwych operacji, gdzie wystarczy wymienić operacje stałoprzecinkowe oraz zmiennoprzecinkowe. Operacje zmiennoprzecinkowe znacząco wykraczają poza ramy cyklu i same w sobie mogą stanowić odrębny cykl. W zakresie operacji logicznych mamy zaledwie kilka operatorów: sumy logicznej, iloczynu logicznego oraz negacji logicznej (czasem do tego dodaje się operacje alternatywy wyłącznej, jednak bazuje ona na operacjach iloczynu, sumy i negacji logicznej), które działają na liczbach w kodzie naturalnym binarnym (oznaczanym jako NB). Tu nie występuje coś takiego jak przeniesienie: dodatkowa informacja wygenerowana w rezultacie wykonania danej operacji na elementach „młodszych”, którą należy uwzględnić w bieżącej operacji (występuje w operacjach wielobajtowych). W zakresie działań arytmetycznych mamy więcej operatorów (jest dodawanie, odejmowanie, mnożenie oraz dzielenie) oraz więcej typów liczbowych (sposobu interpretacji operandów oraz wyników operacji). Poniżej przedstawię podstawowe operacje.

Typy danych

Jak wspomniałem we wstępie, w zakresie operacji arytmetycznych występują różne typy danych. Przez typ danych należy rozumieć sposób interpretacji ciągów bitowych zapisanych w bajtach. Tu wyłania się już pierwszy podział: dane jednobajtowe oraz wielobajtowe. To ma wpływ jedynie na zakres liczbowy. Jak wiadomo, w obrębie bajtu można zapisać 256 różnych kombinacji. W porcji danych zawartych w obszarze dwubajtowym można wykorzystać – rozróżnić ponad 65000 kombinacji.

Na ciąg bitów (bez względu na zajmowaną ilość bajtów) również można spojrzeć z innej perspektywy. Najbardziej naturalną interpretacją jest kod naturalny binarny (NB). Pozwala on zapisać liczby całkowite bez znaku. Nie jest to jedyna możliwa interpretacja w obrębie liczb całkowitych.

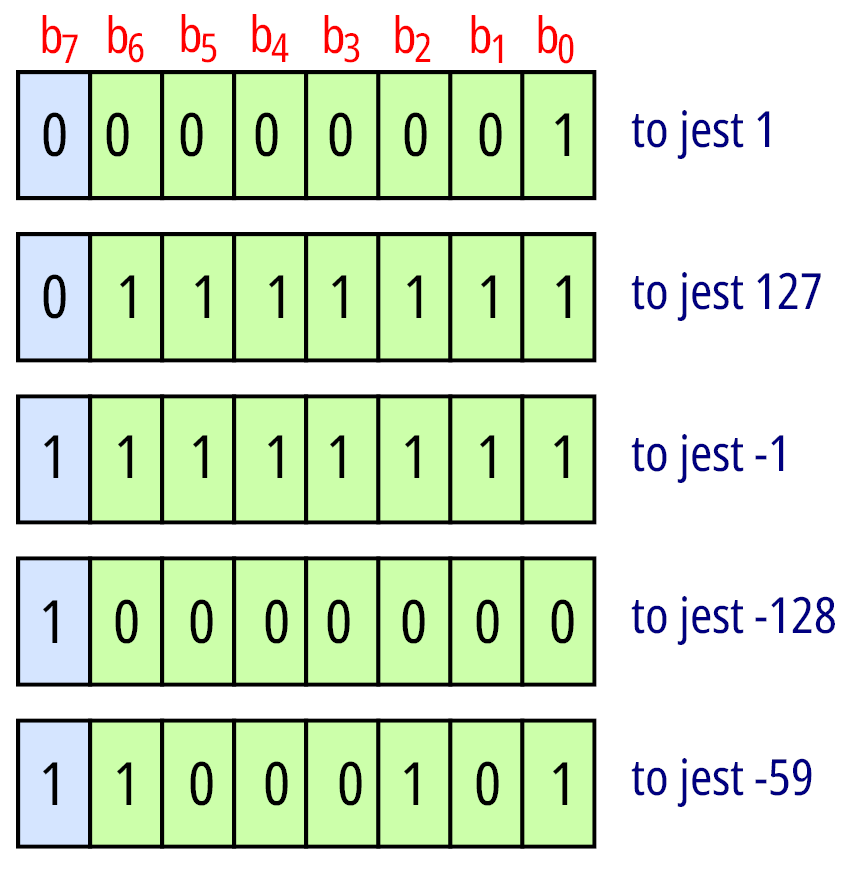
Każdy zapewne dostrzegł, że komputery operują również na liczbach ujemnych. Tak jest w istocie. W takim przypadku bajt (ciąg bajtów) jest interpretowany jako liczba w kodzie uzupełnień do dwóch (w skrócie kod U2). Bit najbardziej znaczący (bajtu jeżeli liczba jest jednobajtowa lub bajtu najbardziej znaczącego jeżeli liczba jest wielobajtowa) jest bitem znaku (0 oznacza liczbę dodatnią, 1 oznacza liczbę ujemną). Pozostałe bity tworzą wartość liczby. Uważny Czytelnik zapewne dostrzegł, że „utrata bitu” na znak liczby ograniczyła zakres liczbowy. I tak i nie. W bajcie na siedmiu bitach maksymalnie można zapisać liczbę 127, więc zakres liczbowy jest mniejszy. Z drugiej strony pojawiły się liczby ujemne. Liczby ujemne łącznie z liczbami dodatnimi wypełniają wszystkie kombinacje, więc ilość liczb w kodzie U2 to 256 sztuk. Skoro liczb dodatnich jest 127, to można przypuszczać, że liczb ujemnych jest tyle samo. No nie jest to prawda, gdyż liczb ujemnych jest więcej o jedną sztukę. W przypadku kodu U2 zapisanego w obrębie bajtu, zakres liczbowy to –128…127. Skąd taka „nierówność”. Wynika ona z tego, że w kodzie U2 jest jedno zero (ciąg bitów 00000000 odzwierciedla właśnie zero – co żartobliwie można nazwać zerem dodatnim: bit znaku jest zerem). Natomiast ciąg 10000000 nie jest zerem „ujemnym”, jest to liczba –128. Mamy 127 sztuk liczb dodatnich, jedno zero i 128 sztuk liczb ujemnych. Kilka przykładów liczb w kodzie U2 pokazuje rysunek 1.

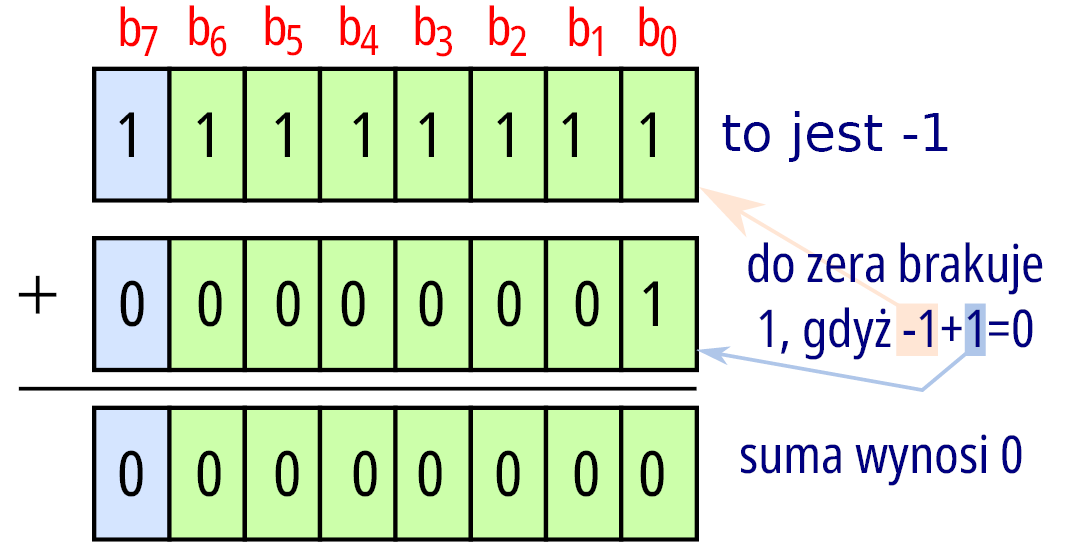
Jak „poznać” wartość liczby w kodzie U2? W przypadku liczb dodatnich będzie to tożsame jak dla liczb w kodzie NB. A dla liczb ujemnych? Należy obliczyć ile „brakuje” do zera. Przykład na rysunku 2.

Jest tu trochę zgadywania, jednak istnieje metoda „analityczna”, która wymaga wykonania dwóch kroków. Należy:

• odwrócić każdy bit liczby (łącznie z bitem znaku),
• do powstałej wartości dodać 1.

(…) ciach!

To jest tylko początek, zapowiedź artykułu, którego pełna wersja ukazała się z numerze kwietniowym czasopisma Zrozumieć Elektronikę (ZE 4/2023). Pełna wersja czasopisma umieszczona jest pod tym linkiem. Natomiast niepełna, okrojona wersja, pozwalająca zapoznać się z zawartością numeru ZE 4/2023 znajduje się tutaj.

 

Andrzej Pawluczuk

apawluczuk@vp.pl