Filtry aktywne – część 3
W poprzednim odcinku zapoznałem Cię z podstawowymi rodzajami filtrów. W wykładzie, podobnie jak w dwóch poprzednich, przekazuję Ci dalsze istotne informacje ogólne o filtrach aktywnych. Dopiero potem podam Ci praktyczne sposoby obliczania podstawowych rodzajów filtrów. Będą to sprawdzone, proste recepty na najpopularniejsze rodzaje filtrów. Bardziej zaawansowani znajdą dodatkowo ogólne wzory, pozwalające dobrać rozmaite kluczowe parametry filtrów.
Jak wspomniałem w pierwszym odcinku, charakterystyka amplitudowa nie charakteryzuje filtru w pełni. W niektórych zastosowaniach bardzo ważna jest charakterystyka fazowa. W jeszcze innych kluczowe znaczenie ma skłonność do „dzwonienia” oraz charakter odpowiedzi na impuls lub ciąg impulsów. W grę wchodzi nie tylko zachowanie filtru w dziedzinie częstotliwości, ale też w dziedzinie czasu.
Aby nad tym wszystkim w pełni zapanować i zaprojektować filtr o pożądanej charakterystyce, trzeba przeprowadzić dość skomplikowane obliczenia. Trzeba wykorzystać matematyczne metody obliczania odpowiedzi filtru na sygnały inne niż sinusoidalne. I właśnie dlatego przy obliczeniach filtrów wykorzystuje się tak zwany rachunek operatorowy. W podręcznikach spotkasz takie określenia jak transformata Laplace’a (czyt. laplasa), bieguny i zera, zmienna zespolona s, zespolona częstotliwość czy zespolona transmitancja. Takie nazwy, parametry, określenia i skomplikowane wzory dotyczące filtrów przerażają większość elektroników. Przystępując do pisania cyklu artykułów o filtrach zaplanowałem sobie pewną kolejność prezentowania materiału. W ramach wprowadzenia, a przed podaniem kolejnych recept, chciałem przedstawić możliwie przystępnie ogólny zarys teorii i oswoić Cię z takimi pojęciami jak bieguny, zera, transmitancje, itp. I te informacje miały być w niniejszym, trzecim odcinku. W trakcie pisania okazało się jednak, że nawet pobieżne wyjaśnienie tych spraw zajęłoby bardzo dużo miejsca – kilka odcinków. Zmieniłem więc plan.
Ty nie bój się wspomnianych pojęć i określeń − na razie nie będą Ci potrzebne. Wystarczy, że przyswoisz sobie podstawowe informacje, konieczne do projektowania prostych, ale jak najbardziej pożytecznych filtrów. Zanim jednak do tego przejdziemy, koniecznie musimy wyjaśnić pewne nieporozumienie dotyczące dobroci i zająć się sprawą podzespołów.
Dobroć filtru
W poprzednim odcinku przypomniałem, że częstotliwości graniczne wyznaczone są przez spadek charakterystyki amplitudowej o 3 dB. To chyba oczywiste!
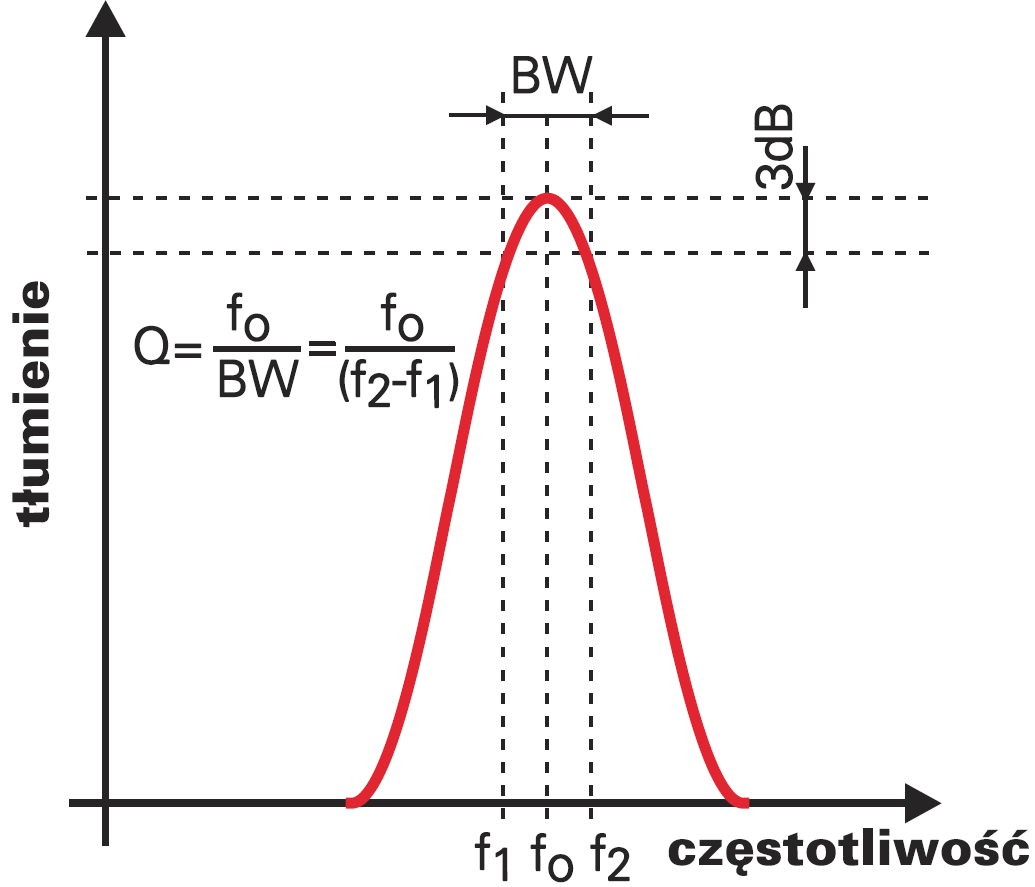
Zapewne wiesz też coś niecoś o dobroci filtrów pasmowych. Dobroć filtru (wąsko) pasmowego to stosunek częstotliwości środkowej i 3−decybelowego pasma przepustowego. Dobroć zwykle oznaczamy literą Q.
Q = fo / BW
gdzie: fo − częstotliwość środkowa, BW (bandwidth), czyli 3−decybelowe pasmo przenoszenia. Ilustruje to rysunek 1. Dla danej częstotliwości środkowej, czym większa dobroć, tym węższe pasmo i tym bardziej stroma charakterystyka.
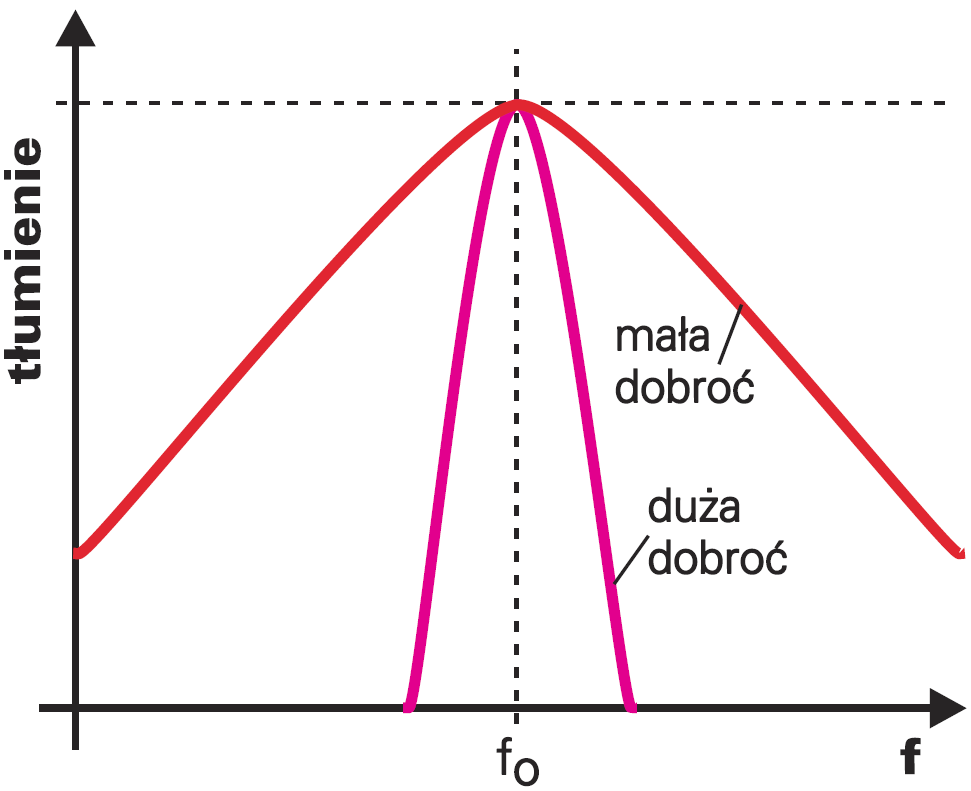
Jeśli spośród wielu różnych sygnałów mamy wydzielić sygnał o jednej, ściśle określonej częstotliwości, potrzebujemy filtru o dużej dobroci. Taki filtr skutecznie stłumi niepożądane sygnały spoza pasma przenoszenia. Rysunek 2 pokazuje przykładowe charakterystyki filtrów pasmowych o tej samej częstotliwości środkowej fo, o małej i dużej dobroci.
W zależności od potrzeb, dobroć filtru środkowoprzepustowego może wynosić na przykład 2, 5 czy 10, a w pewnych przypadkach nawet 100. Dobroć 100 oznacza na przykład, że filtr pasmowy o częstotliwości środkowej 1 kHz będzie miał pasmo przepustowe równe tylko 10Hz. Powiemy, że to bardzo wąski filtr.
Wszystko jasne?
Jak wobec tego rozumieć dobroć filtrów dolno− i górnoprzepustowych?
To nie żarty! Projektując od podstaw filtr aktywny, także dolno− czy górnoprzepustowy, możemy dowolnie wybrać jego parametry, między innymi właśnie dobroć. Oczywiście w przypadku takich filtrów podany wcześniej wzór na dobroć nie ma sensu, ale…
Czy rozumiesz, co to jest dobroć filtru, i jak wpływa na charakterystyki?
Czy filtry powinny mieć jak największą dobroć? Czy dobroć filtrów dolno− i górnoprzepustowych określa stromość charakterystyki amplitudowej?
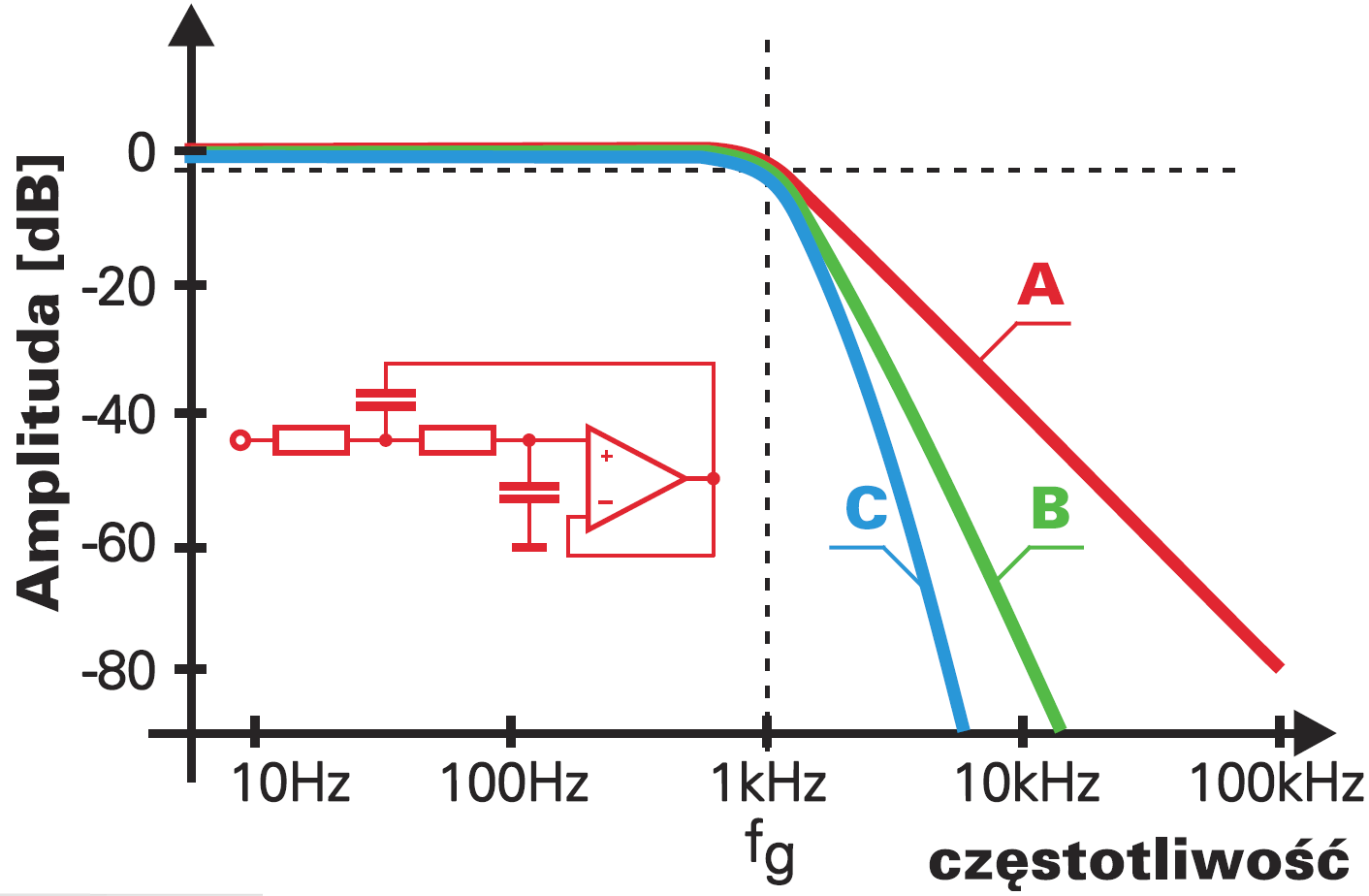
Sprawdź swoją wiedzę w tym względzie za pomocą testu. Popatrz na rysunek 3. Czy z filtru dolnoprzepustowego pokazanego na rysunku, o charakterystyce oznaczonej A (krzywa czerwona) można przez zwiększenie dobroci uzyskać charakterystykę B (krzywa zielona) lub C (niebieska)?
I tu pojawia się pewien pogląd, równie błędny jak popularny − tak właśnie wyobraża to sobie wielu początkujących.
Jeśli Ty uważasz, że nie można, masz rację! Dobroć ma niewielki związek ze stromością charakterystyki. Charakterystyka B o stromości 80 dB/dekadę dotyczy filtru czwartego rzędu, a charakterystyka C – szóstego rzędu (120 dB/dek). Nie można jej uzyskać w filtrze drugiego rzędu przez zwiększenie dobroci, trzeba zastosować dwa albo trzy typowe „moduły” mające stromość po 40 dB/dekadę.
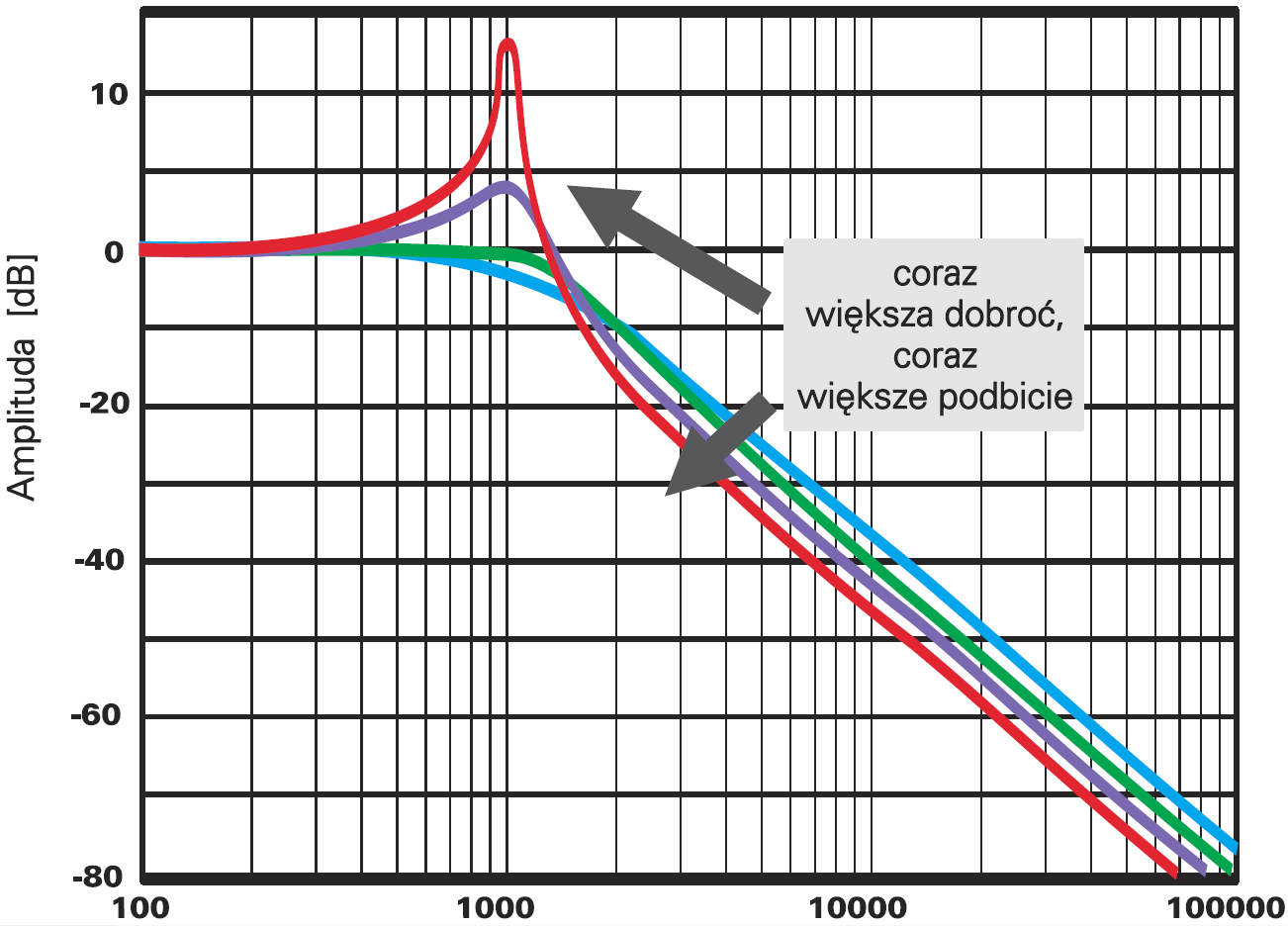
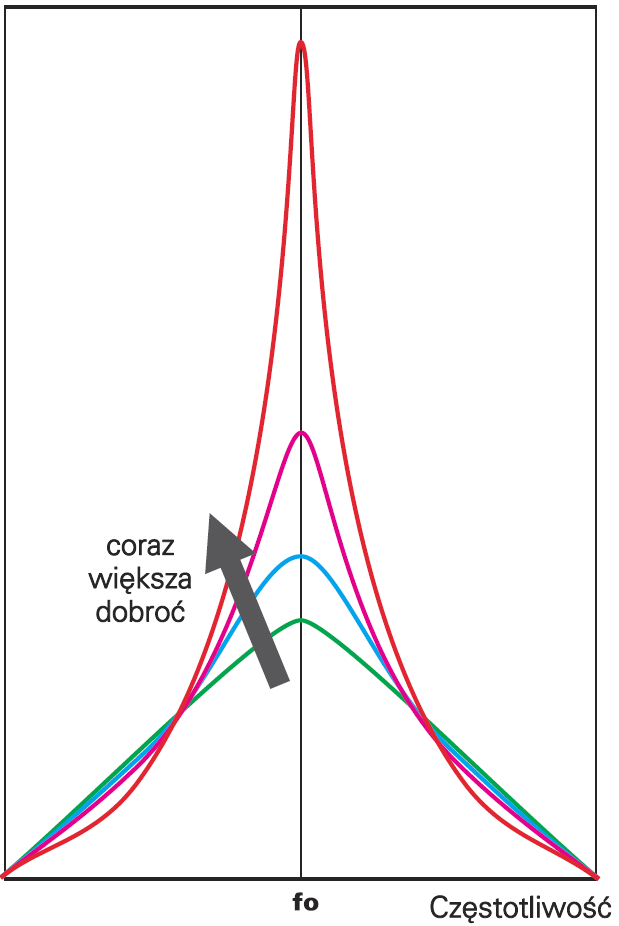
Co więc daje zwiększenie dobroci filtru? Zwiększenie dobroci powoduje zwiększenie skłonności do „dzwonienia” oraz wystąpienie szkodliwego podbicia w okolicach częstotliwości granicznej. Pokazuje to rysunek 4. Owszem, charakterystyka w paśmie zaporowym staje się nieco lepsza, bo leży troszkę niżej, jednak stromość w paśmie zaporowym nadal pozostanie równa 40 dB/dekadę.
Zasadniczo związek wielkości podbicia charakterystyki amplitudowej ze skłonnością do „dzwonienia” dotyczy wszelkich filtrów, także pasmowych. Pokazuje to w pewnym uproszczeniu rysunek 5.
Z „prostego” filtru o dobroci 0,5…0,7 (krzywa zielona), przez zwiększenie dobroci uzyskuje się podbicie charakterystyki, a przy okazji coraz węższe 3−decybelowe pasmo przenoszenia. Przykładowy filtr, gdzie przebiegi wyglądają jak na rysunku 2b ma większą dobroć, niż filtr z przebiegami według rysunku 2a (rysunki dotyczą poprzedniego wykładu) .
Skłonność do „dzwonienia” wcale nie jest pożądana, a często wręcz jest zdecydowanie szkodliwa. Dotyczy to na przykład układów (np. modemów), gdzie trzeba wykrywać krótkie „paczki impulsów” o określonej częstotliwości oraz przerwy między nimi. Długo „dzwoniący” filtr uniemożliwi zidentyfikowanie krótkich przerw między „paczkami impulsów”. Do takich zastosowań filtr o dużej dobroci po prostu się nie nadaje.
Już tu widać, że duża dobroć często nie jest zaletą, tylko poważną wadą. Zapamiętaj raz na zawsze – zwiększanie dobroci filtrów dolno− i górnoprzepustowych powyżej 0,707 powoduje powstanie podbicia charakterystyki w okolicach częstotliwości granicznej oraz zwiększa skłonności do „dzwonienia”.
Nieprzypadkowo bardzo często wykorzystujemy filtry dolno− i górnoprzepustowe o dobroci:
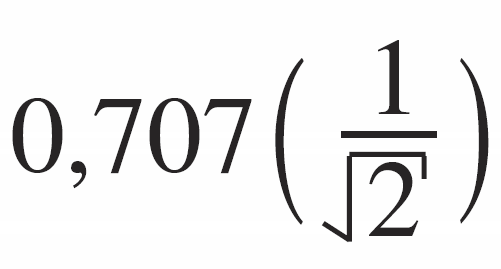
bo mają one najbardziej płaską charakterystykę amplitudową w paśmie przepustowym – to wspomniana wcześniej charakterystyka Butterwortha. Przy dobroci 0,5 otrzymujemy filtr o tak zwa− nym tłumieniu krytycznym – zwany filtrem Bessela (Thomsona). Gdy natomiast najważniejsza jest stromość charakterystyki i gdy możemy dopuścić pewne podbicie w okolicach częstotliwości granicznej możemy trochę zwiększyć dobroć, uzyskując filtr Czebyszewa. Przy dobroci około 1,3..1,4 podbicie będzie wynosić około +3 dB, a tendencje do „dzwonienia” nie będą znaczące. W praktyce prawie nie używamy filtrów dolno− i górnoprzepustowych drugiego rzędu o dobroci większej niż 1,5. Ogniwa o większej dobroci wchodzą jedynie w skład niektórych bardziej skomplikowanych filtrów wyższych rzędów, ale to inna historia.
W każdym razie dzięki temu możemy znakomicie uprościć obliczenia, ograniczając je do filtrów drugiego rzędu i najpopularniejszych wartości: Q=0,5, Q=0,707 oraz Q ~ 1,35, gdy podbicie charakterystyki amplitudowej wynosi około +3 dB.
Wartości dobroci większe niż 1,5 będziemy stosować tylko w przypadku filtrów pasmowoprzepustowych. Tu sprawa jest nieco inna. Projektując filtr pasmowy często chcemy uzyskać wąskie pasmo, co można bardzo łatwo osiągnąć przez zwiększenie dobroci, a skłonność do „dzwonienia” nam nie przeszkadza. W przypadku filtrów LC małej częstotliwości zwiększenie dobroci zwykle jest poważnym problemem ze względu na rezystancję cewki i straty w rdzeniu cewki. W filtrach aktywnych zwiększenie dobroci nie napotyka na większe przeszkody.
Nie znaczy to, że zwiększanie dobroci jest idealnym i uniwersalnym sposobem na uzyskanie filtru w bardzo wąskim paśmie przepustowym. Gdy skłonność do „dzwonienia” nie jest wadą, wtedy wystarczy jeden „moduł” filtru o dużej dobroci. W innych przypadkach, gdy skłonność do „dzwonienia” przekreśla możliwość użycia takiego filtru, trzeba zbudować filtr, zawierający kilka „modułów” o niewielkiej dobroci − wypadkowa charakterystyka amplitudowa będzie podobna, a skłonność do „dzwonienia” − radykalnie mniejsza. Moduły mogą być dostrojone do tej samej częstotliwości, ale zazwyczaj lepiej jest rozsunąć minimalnie częstotliwości modułów, co pozwala uzyskać jeszcze korzystniejszą charakterystykę. Szczegóły wykraczają poza zakres naszego cyklu, w każdym razie uczulam na problem „dzwonienia”, bo jest to zagadnienie zupełnie niedoceniane przez amatorów.
Na marginesie dodam, że filtr o dużej dobroci zachowuje się jak generator drgań gasnących. Natomiast filtr o dobroci równej nieskończoności jest jednocześnie… generatorem przebiegu sinusoidalnego.
Tyle o dobroci. W następnym odcinku podam Ci garść uwag na temat podzespołów.
Piotr Górecki