Elektronika (nie tylko) dla informatyków (14) Kondensatory z lotu ptaka

W poprzednim wykładzie skupiliśmy się na zastosowaniu kondensatorów w roli filtru. W tym wykładzie spojrzymy na te elementy bardziej ogólnie.

Z lotu ptaka…

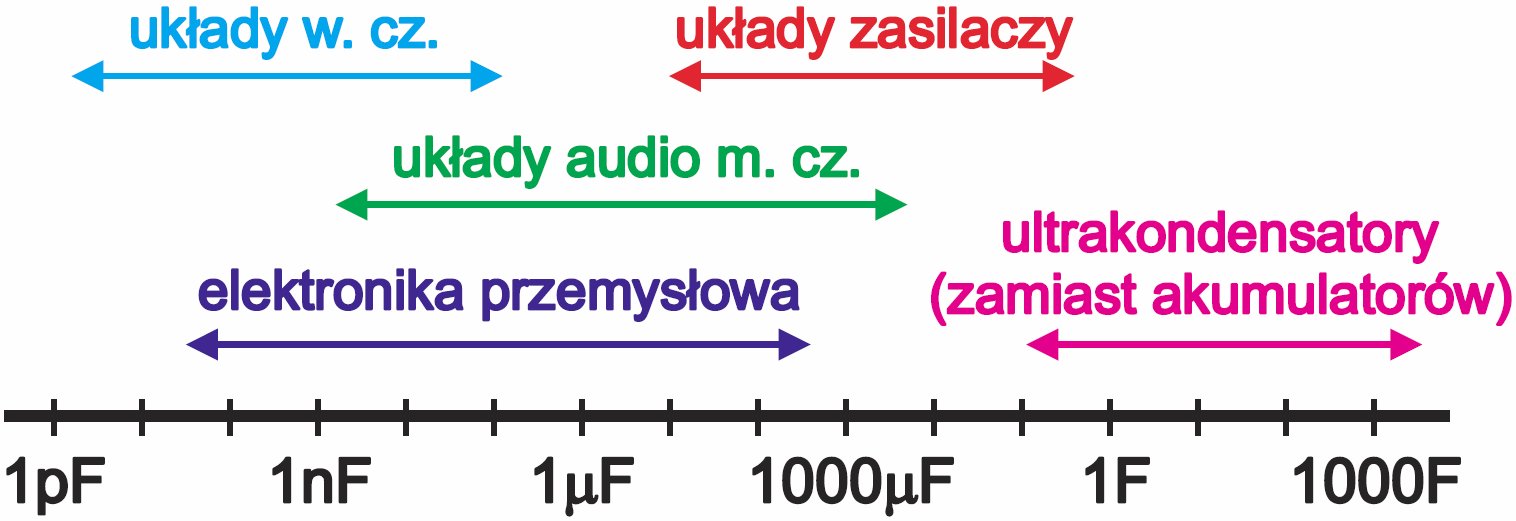
W rozmaitych układach elektronicznych mamy do czynienia z przebiegami o częstotliwościach od ułamków herca do wielu megaherców. Nic dziwnego, że zależnie od zastosowania, wykorzystujemy kondensatory o różnej pojemności.

Czy jest dla Ciebie jasne, że czym wyższa częstotliwość pracy układu, tym mniejsze są pojemności występujących tam kondensatorów? I tak na przykład w zakresie częstotliwości radiowych najczęściej stosuje się kondensatory o pojemnościach od pojedynczych pikofaradów do kilkudziesięciu nanofaradów. Z kolei w zakresie częstotliwości akustycznych najczęściej wykorzystujemy kondensatory o pojemnościach od 1 nanofarada do kilku tysięcy mikrofaradów. W układach zasilających wykorzystuje się pojemności od kilkudziesięciu mikrofaradów do ponad 100 000 mikrofaradów. Ilustruje to rysunek 1.

Wprawdzie nie można ściśle wyznaczyć zakresu częstotliwości pracy dla kondensatora o danej pojemności, jednak z kilku względów dla każdego kondensatora możemy wskazać przybliżony zakres częstotliwości jego pracy. Ta ogólna zależność pojemności od częstotliwości pracy być może jest dla Ciebie oczywista, jednak między innymi warto zwrócić uwagę na wielkość reaktancji X_C kondensatorów, a na dodatek powiązać ją ze współpracującymi rezystancjami.

Zastanów się na przykład, po co nam w układzie kondensator, który przy danej częstotliwości pracy będzie miał reaktancję X_C powyżej 10 megaomów? Tak duża reaktancja to praktycznie przerwa. Inaczej mówiąc, taki kondensator zapewne nic nie zmieni w układzie, czyli tak jakby go nie było. Z drugiej strony, jeśli reaktancja kondensatora przy danej częstotliwości pracy wynosi, powiedzmy, 0,1 oma, to dla przebiegów zmiennych praktycznie stanowi to zwarcie. Zapewne zgodzisz się, że dalsze zmniejszenie tej reaktancji, na przykład do 0,001 oma, nie ma praktycznego sensu i uzasadnienia (a ze względów, które omówimy później, jest po prostu niemożliwe).

Już tu widać, że reaktancja kondensatorów powinna być porównywalna z rezystancjami, występującymi w układzie. Przyjrzyjmy się temu bliżej. Otóż kondensatory bardzo często pracują w obwodach RC, gdzie w sumie pełnią rolę filtrów. Zapewne pamiętasz, że w filtrach RC przy częstotliwości granicznej wartość reaktancji kondensatora jest liczbowo równa rezystancji współpracującego rezystora. W zakresie małych częstotliwości te współpracujące rezystancje najczęściej są rzędu kiloomów, ale mogą mieć wartości od 10 Ω do 1 MΩ. Natomiast w zakresie częstotliwości radiowych współpracujące rezystancje są generalnie mniejsze – tam z różnych względów nie stosuje się rezystancji rzędu megaomów, natomiast bardzo popularnymi opornościami są 50 Ω i 75 Ω. Warto mieć pojęcie, jaka pojemność ma taką reaktancję X_C przy różnych częstotliwościach. Przykładowo przy częstotliwości pracy modułów radiowych 433 MHz reaktancję X_C = 50Ω ma pojemność 7,3 pF:

C = 1 / 2π×f×X_C          C = 1 / 2π×433 MHz×50 Ω           C = 0,159 / 433 MHz×50 Ω

Częstotliwość podaliśmy w megahercach, wynik wyjdzie w mikrofaradach C = 0,0000073 uF czyli właśnie C = 7,3 pF.

Przy częstotliwości radia CB 27,18 MHz reaktancję X_C = 50 Ω ma pojemność 117 pF. Przy krótkofalarskiej częstotliwości 3,5 MHz reaktancję X_C = 50 Ω ma pojemność 909 pF. Przy częstotliwości 20 kHz reaktancję X_C = 50 Ω ma pojemność 159 nF. Przy małej częstotliwości audio 1 kHz reaktancję X_C = 50 Ω ma pojemność 3,18 uF. Przy 20 Hz reaktancję X_C = 50 Ω ma pojemność 159 uF.

Te informacje dobrze ilustrują podstawową zależność, że czym mniejsza częstotliwość pracy, tym większe pojemności będą mieć kondensatory w układzie. Wprawdzie moglibyśmy doszukiwać się wyjątków, które w istocie wyjątkami nie są: na przykład w sprzęcie audio spotyka się też kondensatory o pojemności 100 pF, a nawet mniejszej – jednak ich zadaniem jest wpływanie na charakterystykę w zakresie najwyższych częstotliwości i zapobieganie samowzbudzeniu na wysokich częstotliwościach ponadakustycznych i stąd tak mała pojemność. Z kolei na przykład w urządzeniach radiowych wysokiej częstotliwości, tak jak wszędzie, stosuje się duże kondensatory elektrolityczne, jednak nie pracują one w torach sygnału w.cz., tylko w obwodach zasilania, gdzie pełnią rolę magazynów energii.

Mógłbyś też zapytać, dlaczego pomijamy pojemności rzędu 1 pF i mniejsze? Przecież dziś nawet hobbyści mają do czynienia z układami o częstotliwościach pracy ponad 1 GHz, np. w radiokomunikacji amatorskiej w paśmie 5 GHz czy urządzeniach techniki satelitarnej w zakresie 10…12 GHz. Nietrudno policzyć, że na przykład przy popularnej częstotliwości radiowej 2,4 GHz (Wi-Fi, Bluetooth), kondensator o pojemności 1 pF miałby niewielką reaktancję, nieco ponad 66 Ω…

W zasadzie tak, ale w grę wchodzą tu co najmniej dwie kwestie. Po pierwsze rozmaite szkodliwe pojemności, w tym pojemności montażowe, bardzo często mają wartości większe niż 1 pF. Jak pokazuje fotografia 2, dwa niewielkie skręcone druciki w izolacji PCV mają pojemność 1,8 pF. Po drugie, przy wysokich częstotliwościach wchodzą w grę tak zwane zjawiska falowe. W zasadzie zjawiska falowe zachodzą także przy małych częstotliwościach, ale w praktyce dają o sobie znać dopiero wtedy, gdy długość fali jest porównywalna z rozmiarami układu czy linii przesyłowej (a dla częstotliwości 2,4 GHz długość fali wynosi 12,5 cm w próżni, jednak gdy dielektrykiem jest laminat FR4 to długość fali zmniejsza w przybliżeniu się jeszcze o połowę). Mówiąc w skrócie, pojęcie reaktancji pojemnościowej, a nawet pojemności traci wtedy znaczenie. Choćby z tych względów nie mamy do czynienia z kondensatorami o pojemności poniżej 1 pF, choć takie pojemności w układach występują.

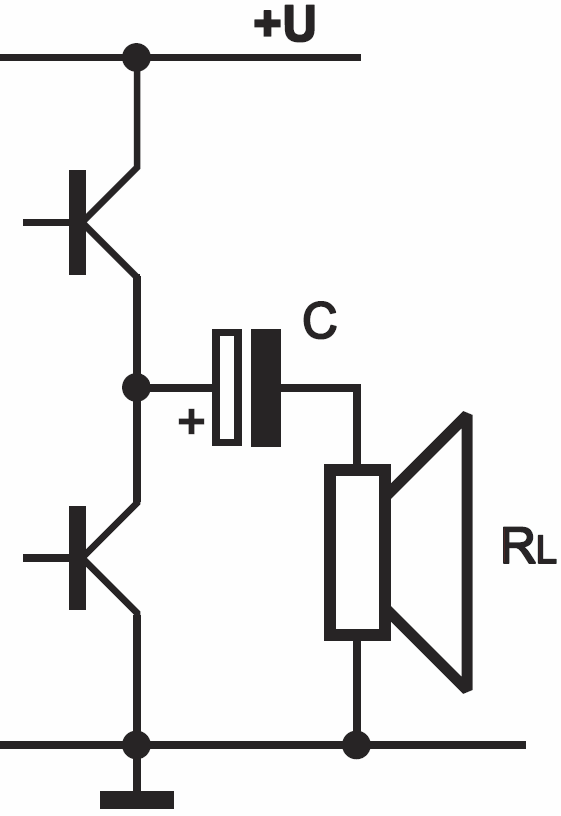
A jeśli chodzi o największe pojemności, to sprawa ma jeszcze inne oblicze. Jak wiesz, kondensatory o dużej pojemności, powiedzmy co najmniej 100 uF, stosowane są przede wszystkim jako pomocnicze, niejako wspomagające źródła energii w zasilaczach i w ogóle w obwodach zasilania. Jeśli chodzi o przypadki obliczania reaktancji przy najmniejszych częstotliwościach, to jest ich niezbyt wiele. I tak na przykład hobbystę interesuje oporność kondensatorów wyjściowych we wzmacniaczach audio zasilanych pojedynczym napięciem. Na wyjściu takiego wzmacniacza, w szereg z głośnikiem, musi być włączony kondensator (rysunek 3) i przy najniższej częstotliwości pracy jego reaktancja X_C nie powinna być większa od oporności głośnika R_L.

Policzmy to dla głośnika 4 Ω i częstotliwości 20 Hz:

C = 0,159 / (4 Ω×20 Hz)          C = 0,159 / 80 = 0,159 / (4 Ω×20 Hz)          C = 1987,5 uF

Przy tej pojemności C , reaktancja X_C ma wartość 4 Ω.

W praktyce do głośnika 4-omowego wystarczy kondensator 2200 uF, natomiast nie ma potrzeby zwiększania pojemności takiego kondensatora wyjściowego powyżej 4700 uF. Dla głośnika 8 Ω wystarczy pojemność 1000 uF…2200 uF. Zauważ, że moc wzmacniacza i głośnika nie ma tu znaczenia – po prostu przy dużych mocach kondensator wyjściowy będzie pracował przy wyższym napięciu.

Praktyczne obliczenia

Elektronik dość często musi obliczać reaktancję pojemnościową.

Nie zawsze trzeba wykorzystywać kalkulator i wzór X_C = 0,159 / fC

Najczęściej wystarczy z grubsza oszacować reaktancję X_C. Wielu praktyków zapamiętuje, jaką reaktancję ma kondensator 1 uF przy częstotliwości 1 kHz i potem w uproszczony sposób przelicza dla innych częstotliwości i pojemności, pamiętając, że najczęściej wykorzystywane kondensatory mają nominały będące (pod)wielokrotnością 1, 2,2 oraz 4,7, czyli w przybliżeniu 1, 2, 5. Jest oczywiste, że ten sam kondensator przy częstotliwości 10 razy większej będzie miał reaktancję 10 razy mniejszą. Z kolei przy tej samej częstotliwości kondensator o pojemności np. 5 razy większej będzie miał reaktancję 5 razy mniejszą.

Trzeba też pamiętać, że 160 pomnożone przez 2 daje 320, a podzielone przez 5 daje 32. Z kolei 160 pomnożone przez 5 daje 800, a podzielone przez 2 daje 80. Co ważne, takie szacunkowe obliczenia warto przeprowadzać dla „okrągłych” wartości częstotliwości, też będących wielokrotnościami 1, 2, 5. Zauważ, że wtedy w obliczeniach będziemy mieć do czynienia z jedynie wielokrotnościami liczb 1,6, 3,2, 4 oraz 8.

Zapamiętaj więc raz na zawsze: kondensator 1 uF przy częstotliwości 1 kHz ma reaktancję 160 Ω.

Proponowane oszacowania można bardzo szybko zrobić w pamięci lub na kartce, jak w poniższych przykładach. Sprawdźmy więc szybciutko, jaką reaktancję będzie miał kondensator 47 nF (50 nF) przy częstotliwości 20 Hz:

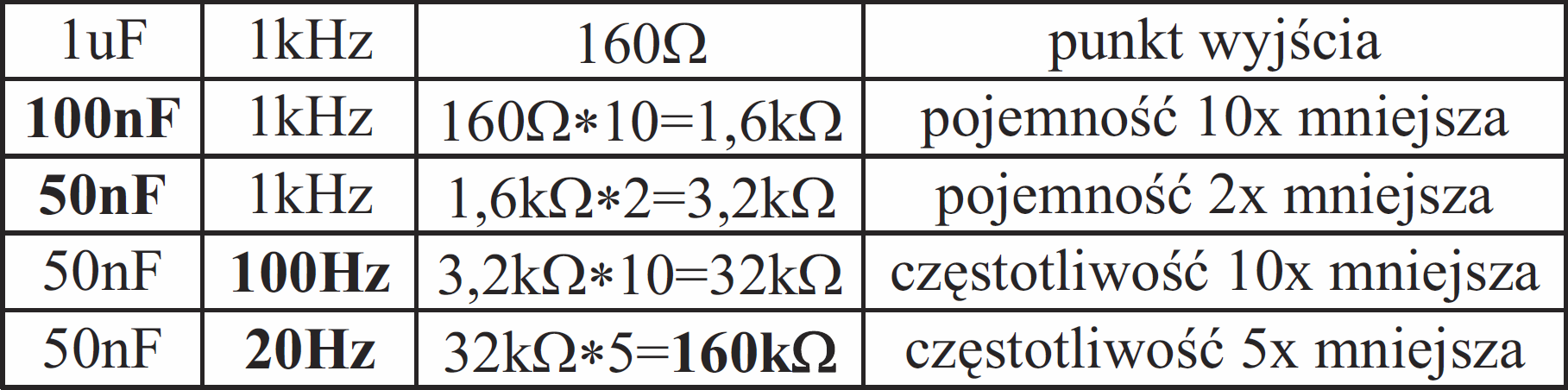
lub to samo w innej kolejności:

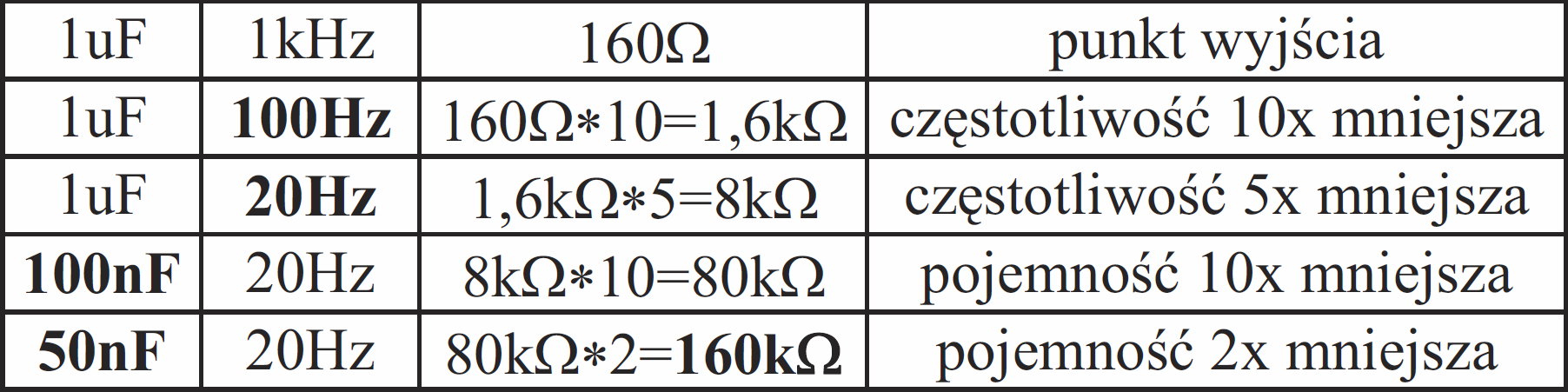
Inny przykład: obliczamy reaktancję kondensatora o pojemności 220 pF (200 pF) przy częstotliwości 200 kHz:

Jest to naprawdę prosty i pożyteczny sposób, do którego też łatwo się przyzwyczaić. W ogromnej większości przypadków, takie uproszczone wyliczenia całkowicie wystarczą. A teraz omówimy bardzo ważną kwestię:

Jak Zwiększyć pojemność?

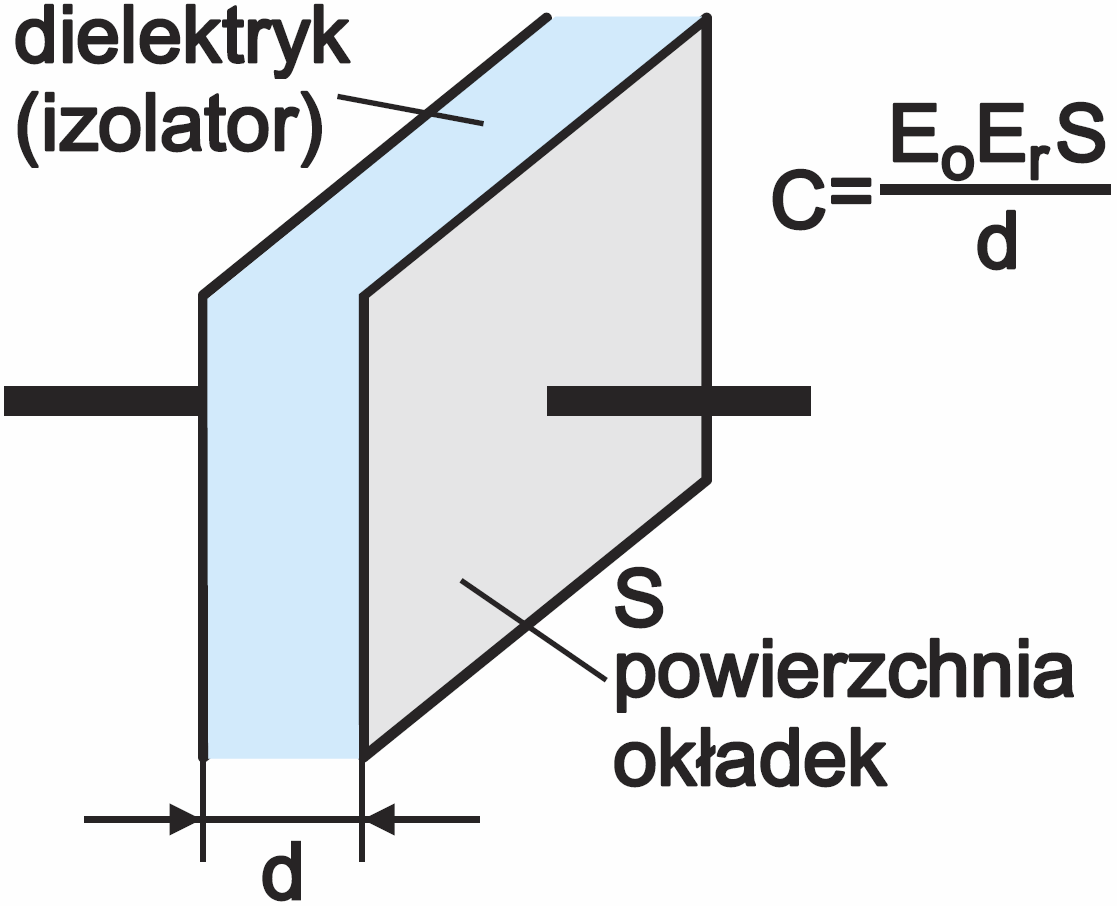
Powróćmy do podstawowego, szkolnego przykładu kondensatora płaskiego (rysunek 4) i wzoru na jego pojemność:

C = ε₀ε_rS / d

gdzie: ε₀ – przenikalność elektryczna próżni (ε₀=8,854×10^–12F/m), ε_r – względna przenikalność elektryczna dielektryka, S – powierzchnia okładek kondensatora, d – odległość między okładkami.

Nietrudno policzyć, że kondensator złożony z dwóch metalowych płytek 10×10 cm (0,1×0,1 m) oddalonych o 1 mm (0,001 m) z dielektrykiem powietrznym (ε_r = 1) ma żałośnie małą pojemność około 88,5 pF. Fotografia 5 pokazuje, że zmierzona multimetrem pojemność kondensatora w postaci płytki z laminatu dwustronnie miedziowanego 6,5×5,2 cm wynosi około 100 pF. Tymczasem w elektronice potrzebujemy kondensatorów o pojemności tysięcy, milionów, miliardów, a nawet bilionów (!) razy większych. Na dodatek powinny to być kondensatory o możliwe małych rozmiarach!

Jak można zwiększyć pojemność kondensatora? Przenikalności elektrycznej próżni ε₀ zmienić się nie da, jednak można zwiększyć pojemność przez:

(1) zastosowanie dielektryka o jak największej przenikalności względnej ε_r. O ile dla próżni i powietrza przenikalność względna wynosi 1, o tyle niektóre rodzaje ceramiki (tzw. ferroelektryki) mają przenikalność dziesiątki tysięcy razy większą. Mamy więc pierwszy sposób na zwiększanie pojemności. Inna droga do uzyskania dużej pojemności, to:

(2) zwiększenie powierzchni okładek S, a kolejna to:

(3) zmniejszenie odległości między okładkami d.

Tylko w teorii jest to proste. Do uzyskania dużych pojemności trzeba sprytnie wykorzystać wszystkie trzy sposoby. Nietrudno się domyślić, że w tak szerokim zakresie pojemności mamy do czynienia z kondensatorami różnego typu, realizowanych odmiennymi technologiami, z użyciem rozmaitych materiałów.

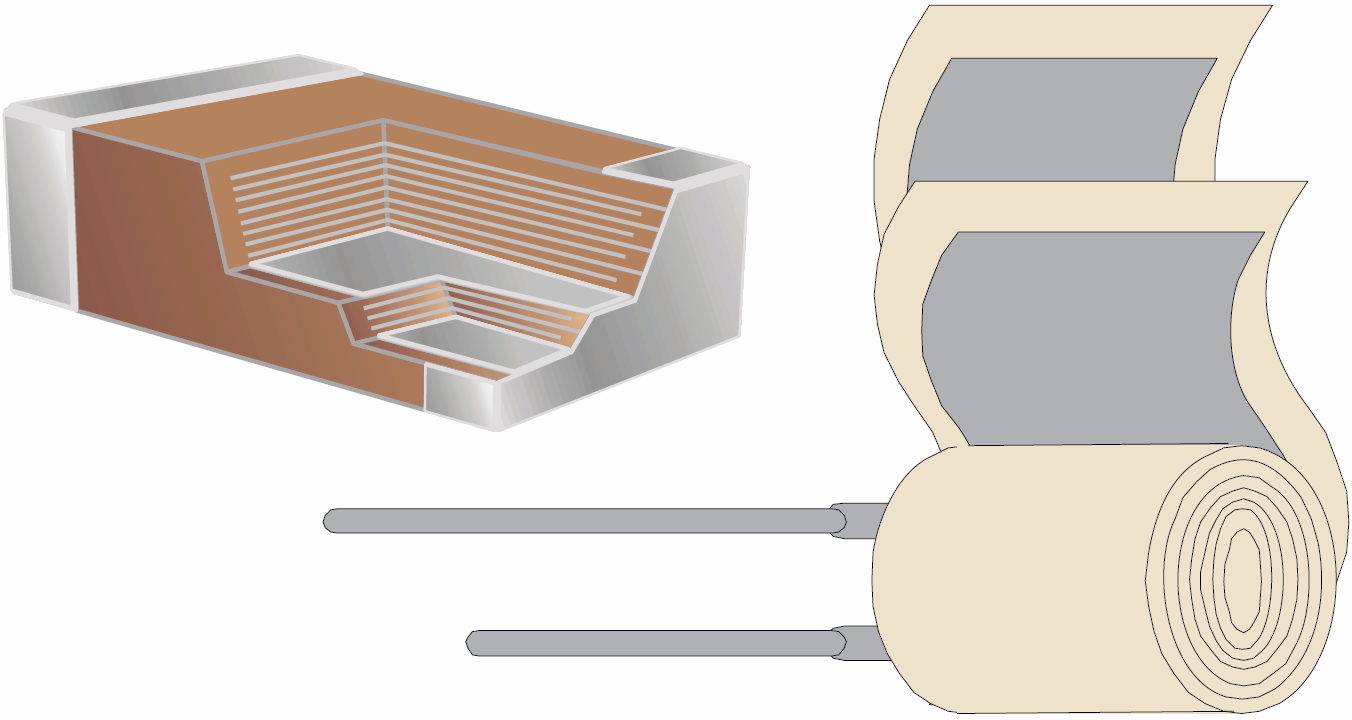
I tak na przykład zwiększenie powierzchni okładek S to nie tylko kwestia stosowania jak największych i jak najcieńszych elektrod (okładzin). Do uzyskania dużych pojemności, znacznie powyżej 1 uF, nie wystarcza stosowanie struktury wielowarstwowej czy zwijanie w rulon elastycznych taśm, jak na rysunku 6.

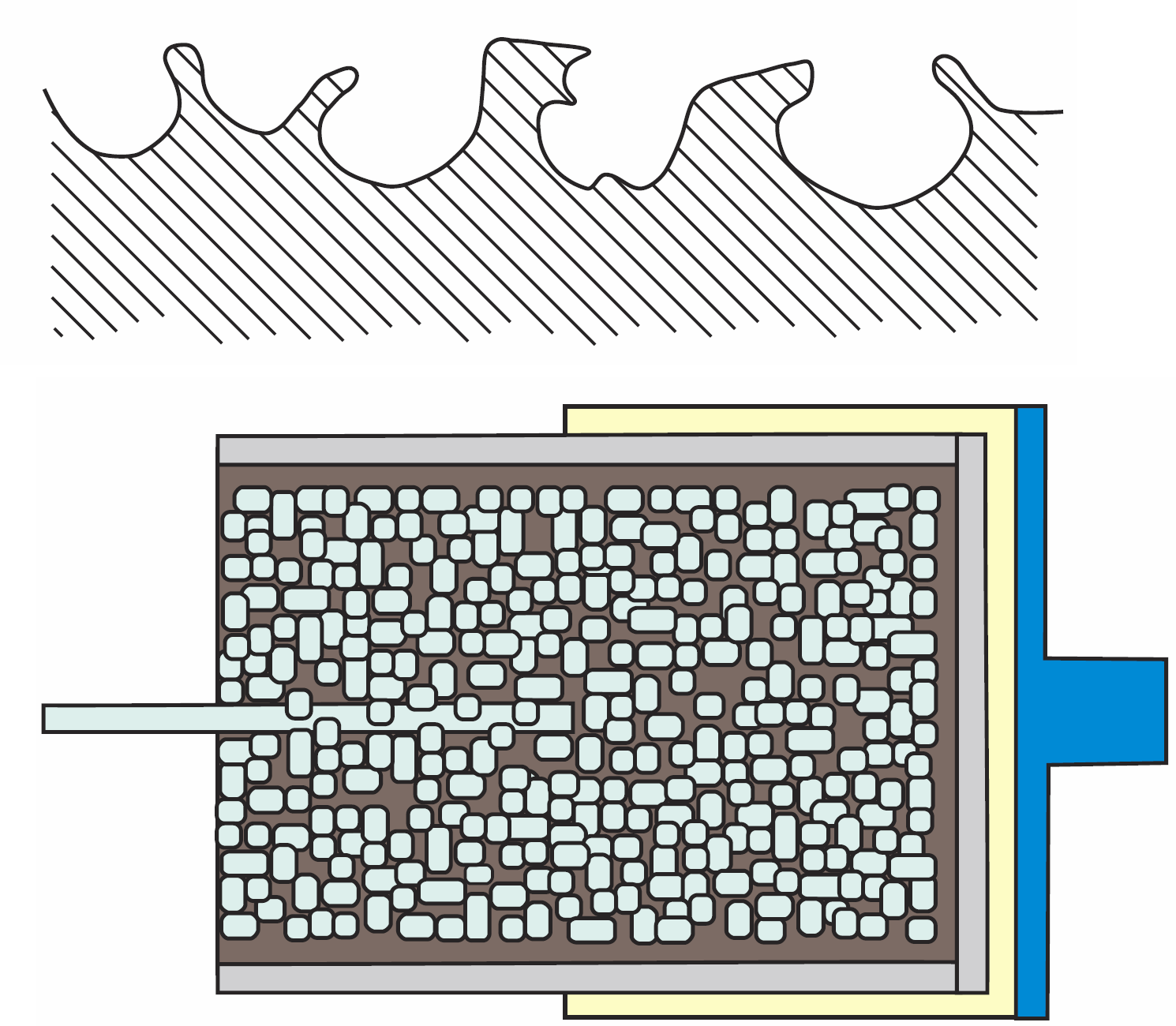
Dla uzyskania bardzo dużych pojemności trzeba uciekać się do niecodziennych metod zwiększania powierzchni czynnej, na przykład polegających na uzyskaniu chropowatej, porowatej powierzchni albo nawet struktury przestrzennej, nieco podobnej do gąbki. Pozwala to wielokrotnie zwiększyć powierzchnię czynną w porównaniu z płaskimi okładkami, co ilustruje w uproszczeniu rysunek 7.

Co istotne, nie można zanadto zmniejszyć odległości d, czyli grubości dielektryka, ponieważ obniży to odporność na przebicie pod wpływem silnego pola elektrycznego. A przebicie dielektryka grozi nieodwracalnym uszkodzeniem – trwałym zwarciem kondensatora. W praktyce napięcie maksymalne to drugi po pojemności najważniejszy parametr kondensatora, a problem przebicia ściśle wiąże się z rodzajem dielektryka i jego grubością.

Tu można wspomnieć, że zaskakujący sposób wykorzystano w ultrakondensatorach – tam grubość dielektryka d jest… równa zeru. Tam w ogóle nie ma dielektryka, tylko na styku dwóch warstw odpowiednio dobranych cieczy lub cieczy i materiału stałego, pełniących rolę okładek, tworzy się swego rodzaju bariera. Stąd między innymi ogromna pojemność, ale właśnie dlatego napięcie maksymalne ultrakondensatorów jest żałośnie małe i wynosi około 2…3 V.

Natomiast w klasycznych kondensatorach dielektryk powinien mieć jak najwyższą odporność na przebicie i jednocześnie jak najwyższą wartość przenikalności względnej ε_r. W praktyce oznacza to, że na dielektryk trzeba starannie wybrać odpowiedni materiał. Musi on mieć potrzebne właściwości elektryczne, a ponadto trzeba opracować technologię produkcji. Jak się jeszcze okaże, są to bardzo poważne wyzwania.

Już podane wiadomości sugerują, że stosowane w praktyce kondensatory nie są idealne, przede wszystkim z uwagi na właściwości dielektryka. Nietrudno się też domyślić, że czym większa pojemność i czym bardziej skomplikowana i niecodzienna jest budowa kondensatora, tym bardziej można się spodziewać rozmaitych wad i szkodliwych parametrów.

Rzeczywiste kondensatory poważnie odbiegają od ideału, ponieważ oprócz króciutko wspomnianych tu przyczyn, w grę wchodzą jeszcze inne, o dużym znaczeniu praktycznym. Zanim je jednak omówimy, koniecznie musimy zapoznać się z indukcyjnością i cewkami. Już teraz zasygnalizuję tylko, że z uwagi na różne niedoskonałości przy bardzo dużych częstotliwościach kondensatory przestają spełniać swą funkcję i zachowują się jak… rezystory, a nawet jak kiepskie cewki. Cewkami zajmiemy się w następnym odcinku. A dopiero potem powrócimy do kondensatorów, ich rodzajów i właściwości.

Piotr Górecki