Elektronika (nie tylko) dla informatyków (15) Cewki i dławiki

W poprzednim wykładzie spojrzeliśmy na kondensatory bardzo ogólnikowo, czyli z lotu ptaka. W tym wykładzie zmieniamy kurs z kondensatorów na cewki.

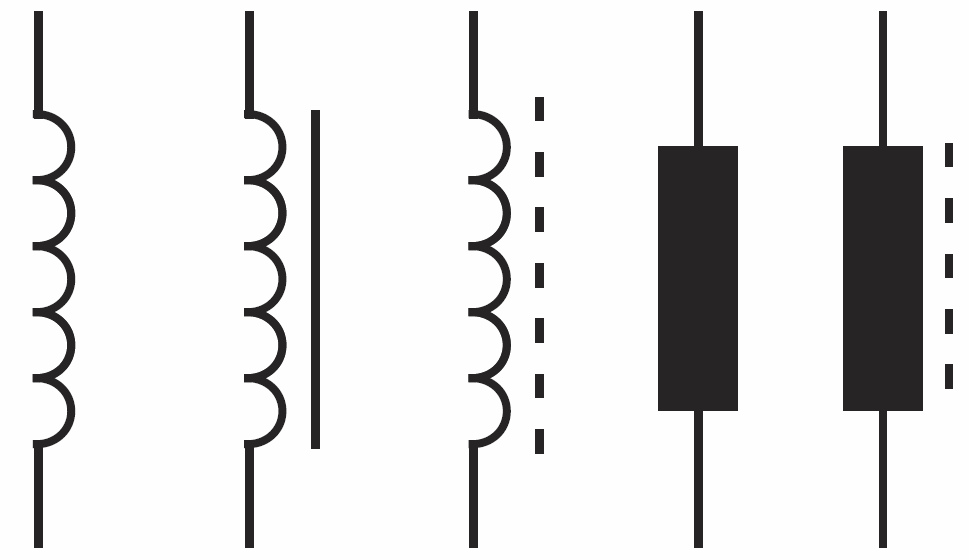
Typowa cewka to wiele zwojów drutu, nawiniętych zwykle na jakimś rdzeniu. Nawiązuje do tego symbol cewki indukcyjnej, pokazany w różnych odmianach na rysunku 1. Cewki i indukcyjność to temat uważany przez wielu za trudny, nieprzystępny, a nawet niepraktyczny.

Faktem jest, że kwestie projektowania i nawijania elementów indukcyjnych do łatwych nie należą. Jednak podstawy okazują się bardzo łatwe, zwłaszcza jeśli świeżo w pamięci mamy podstawowe właściwości kondensatora. Przekonasz się, że cewka i indukcyjność są w pewnym sensie przeciwieństwem, a właściwie dopełnieniem kondensatora i pojemności. Być może po poznaniu szczegółów powiesz, że z cewkami jest dokładnie tak samo, jak z kondensatorami… tylko odwrotnie. Ale znów zacznijmy od wykorzystania analogii hydraulicznej.

Podstawowe właściwości cewki

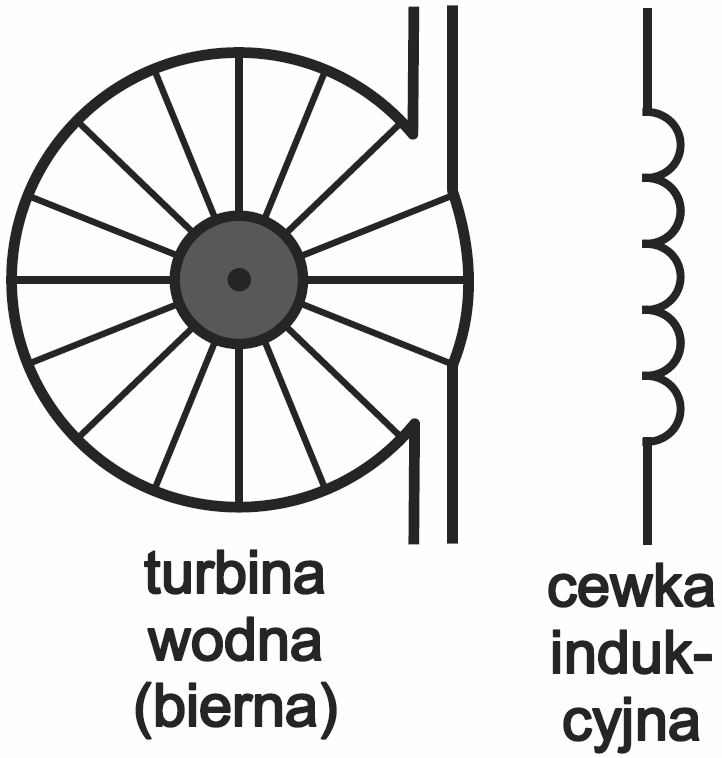
W analogii hydraulicznej odpowiednikiem cewki indukcyjnej jest turbina, rodzaj ciężkiego koła zamachowego – patrz rysunek 2. Turbina ta nie jest napędzana żadnym silnikiem, tylko jest elementem biernym, który może być wstawiony w obwód przepływu wody. Płynąca woda będzie dla takiej turbiny czynnikiem napędzającym, ale po nabraniu prędkości turbina może też pełnić rolę pompy.

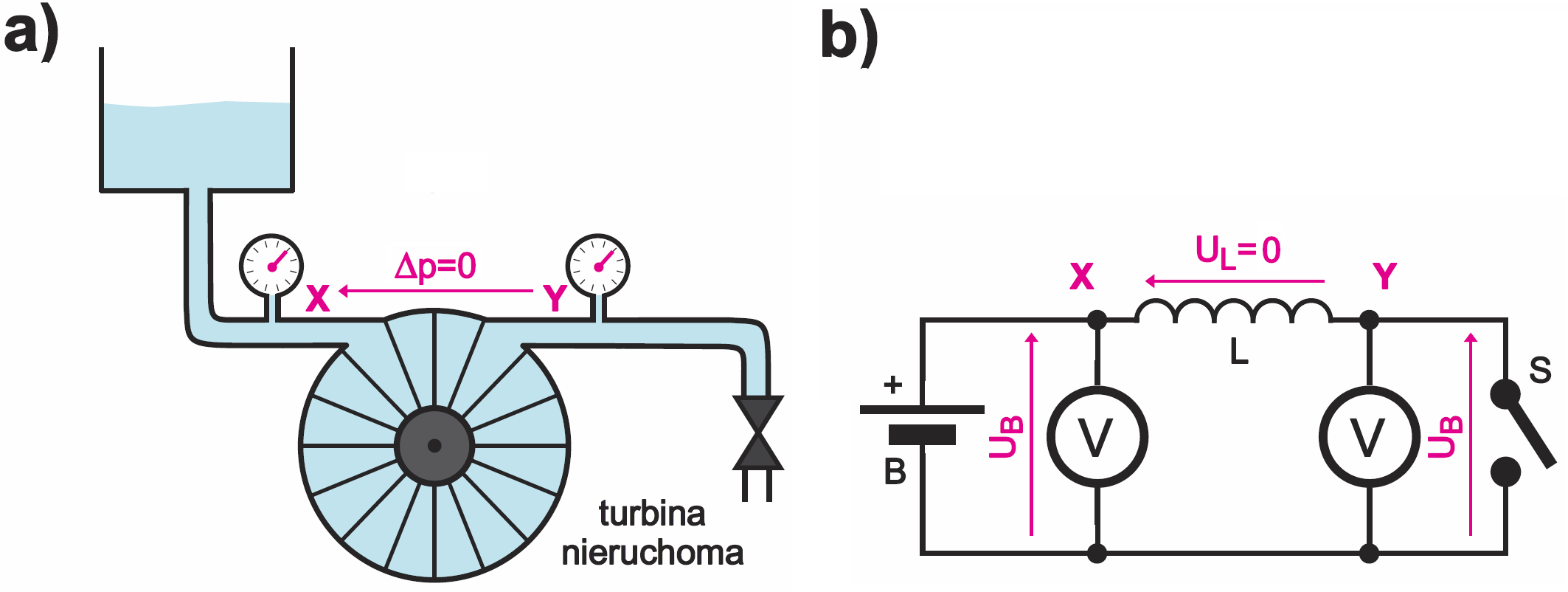
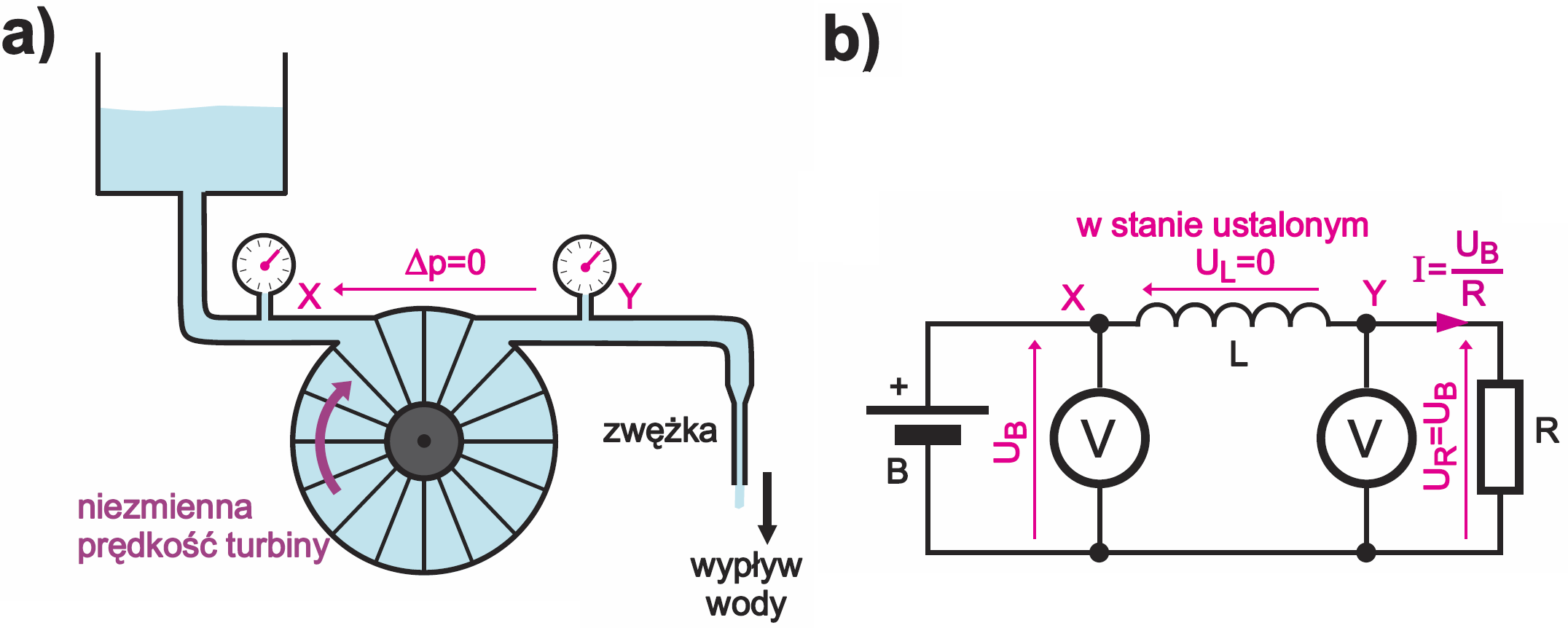
Zastanówmy się nad działaniem takiej turbiny. Załóżmy, że w układzie jak na rysunku 3 zawór jest zakręcony i woda (prąd) w obwodzie nie płynie. Oba mierniki ciśnienia (woltomierze) mają takie same wskazanie – tyle ile wynosi ciśnienie (napięcie) zasilające.

Załóżmy teraz, że w jakiejś chwili t₀ został otwarty zawór S i ciśnienie (napięcie) w punkcie B spadło do zera, jak ilustruje rysunek 4. Czy woda (prąd) od razu popłynie obfitym strumieniem?

 

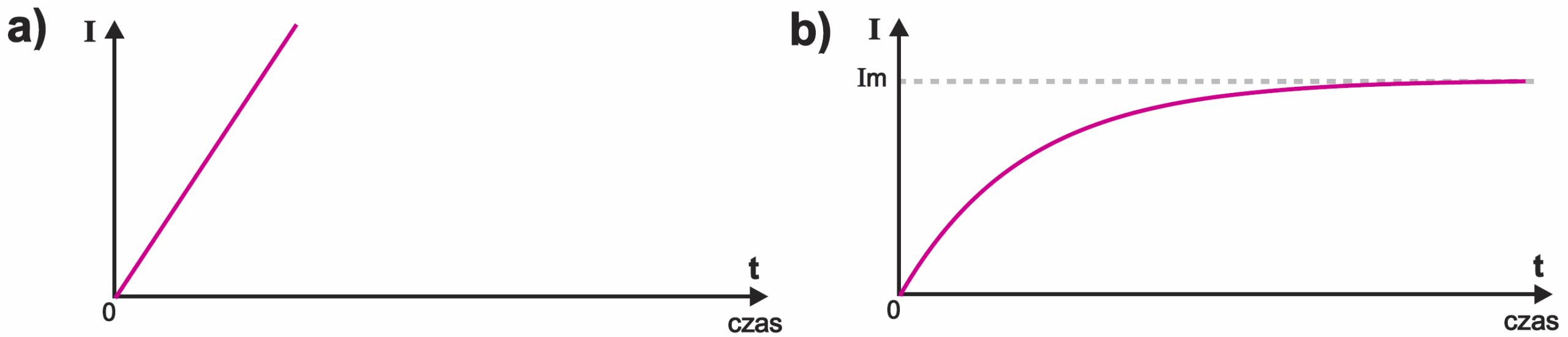
Nie! Przeszkodą będzie nieruchoma turbina z ciężkim kołem zamachowym (cewka indukcyjna). Jednak ciśnienie wody (napięcie) spowoduje, że turbina zacznie się pomału obracać i stopniowo nabierać prędkości, a to umożliwi coraz większy przepływ wody (coraz większy prąd). Miernik ciśnienia (napięcia) w punkcie X cały czas będzie pokazywał ciśnienie (napięcie) zasilające, natomiast po otwarciu zaworu ciśnienie w punkcie Y spadnie do zera. Zwróć uwagę na przepływ wody (prądu) – gdyby źródło zasilania miało nieskończenie wielką pojemność, to przepływ wody (prąd) wzrastałby jednostajnie do nieskończoności, jak pokazuje rysunek 5a. W rzeczywistości narośnie do jakiejś wartości maksymalnej, ograniczonej oporami tarcia (rezystancjami) w obwodzie, jak z rysunku 5b.

 

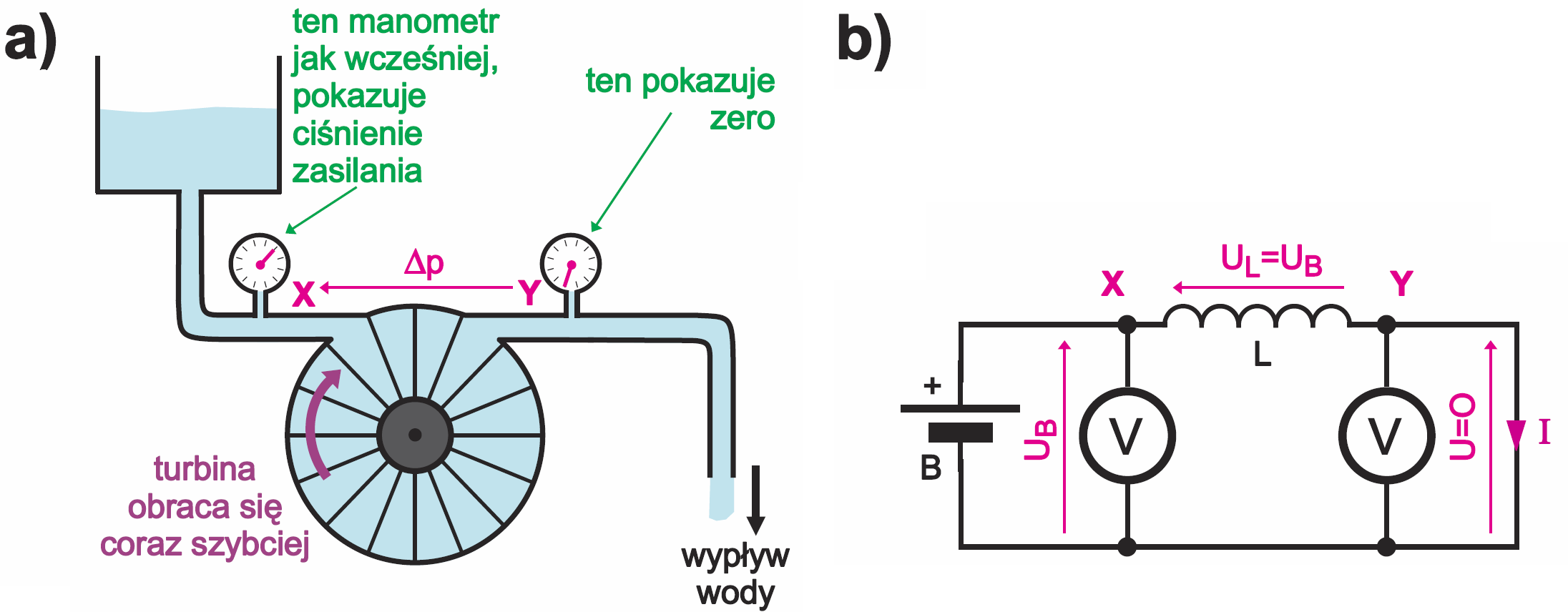
Zastanówmy się teraz nad właściwościami takiego układu z oporami tarcia (rezystancją). W takim układzie po otwarciu zaworu przepływ wody (prąd) będzie wzrastał jak na rysunku 5b i po jakimś dłuższym czasie ustabilizuje się na jakiejś wartości Im, czyli osiągnie stan ustalony. W takim stanie ustalonym wypływ wody (prąd) będzie wyznaczony przez ciśnienie zasilające (napięcie U_B) i opór (rezystancję). Zauważ, że jak ilustruje rysunek 6a, w takim stanie ustalonym turbina będzie się obracać z jakąś stałą prędkością, a co ważne, różnica ciśnień na obu jej końcach będzie równa zeru. Tak samo w obwodzie elektrycznym. Po dłuższym czasie, czyli w stanie ustalonym, prąd osiągnie niezmienną wartość, wyznaczoną przez napięcie U_B i rezystancję R zgodnie z prawem Ohma (I = U/R), jak ilustruje rysunek 6b. I co ważne, w takim stanie ustalonym napięcie na idealnej cewce byłoby równe zeru. Oczywiście tak byłoby wtedy, gdyby turbina (cewka) była idealna, gdyby nie było w niej strat tarcia (rezystancji strat). Na razie pomińmy jednak problem strat i rezystancji cewki.

Być może masz jednak wątpliwości, czy w stanie ustalonym rzeczywiście napięcie na (idealnej cewce) byłoby równe zeru. Wróć do rysunku 3 – tu chyba nie masz wątpliwości: gdy nie płynie prąd, wtedy napięcie na obu końcach cewki są jednakowe, czyli napięcie na cewce jest równe zeru. Podobnie nie ma wątpliwości odnośnie do rysunku 4a: gdy całkowicie utworzymy zawór, to woda nie popłynie od razu gwałtownym strumieniem. Całe ciśnienie zasilające wystąpi na turbinie i ta zacznie się coraz szybciej obracać, stopniowo zwiększając przepływ prądu. Tak samo w układzie elektrycznym według rysunku 4b po zwarciu wyłącznika S na cewce cały czas będzie występować napięcie U_B i właśnie to spowoduje, że prąd będzie liniowo wzrastał. Zauważ, że to właśnie napięcie przyłożone do cewki powoduje narastanie prądu. W analogii hydraulicznej z rysunku 4, czym większe ciśnienie na końcach turbiny, tym szybciej wzrasta prędkość turbiny i przepływ wody. Analogicznie jest w obwodzie elektrycznym: czym większe napięcie na cewce, tym szybciej narasta w niej prąd. Ilustruje to rysunek 7. W tym wypadku warto potraktować napięcie na cewce jako przyczynę, a przepływ prądu i szybkość wzrostu prądu jako skutek.

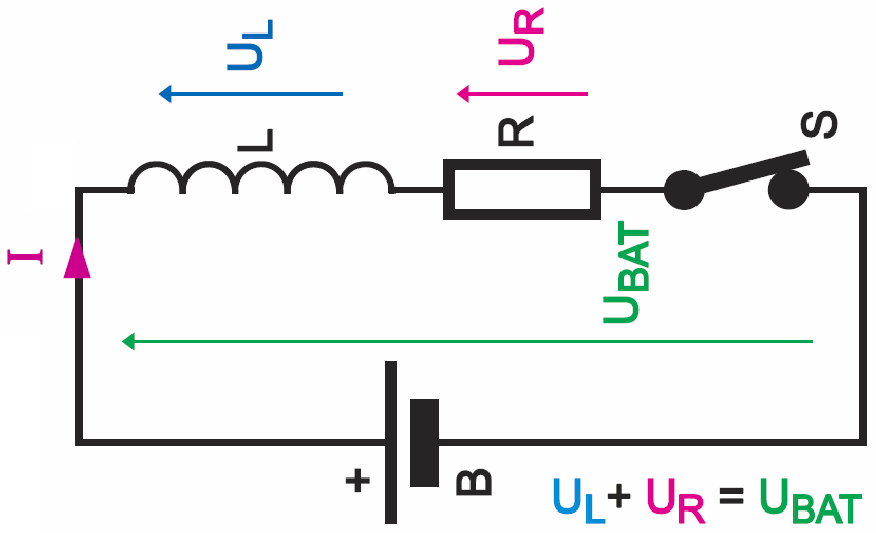
A jeśli czujemy tę prostą i oczywistą zależność, to łatwo możemy przeanalizować sytuację przejściową w obwodzie z rezystancją z rysunku 8. Wcześniej, przy rozwartym wyłączniku S nie było przepływu wody i mieliśmy sytuację dokładnie taką jak na rysunku 3: prąd równy zeru, napięcie na cewce równe zeru, a napięcie na rezystancji równe zeru. Teraz interesuje nas, co będzie się działo w stanie nieustalonym, tuż po zwarciu wyłącznika S. Otóż w pierwszej chwili i tylko w pierwszej krótkiej chwili po zwarciu wyłącznika S wystąpi sytuacja jak na rysunku 4.

W tej pierwszej chwili prąd będzie równy zeru, więc na rezystorze napięcie też będzie równe zeru (U=I×R) i całe napięcie baterii wystąpi na cewce (U_L=U_BAT). Ale tak będzie tylko w pierwszej chwili po zwarciu wyłącznika S. Potem zgodnie z rysunkami 5 i 7 zacznie narastać prąd. Ten prąd będzie oczywiście płynął przez rezystor R i wywoływał na nim coraz większy spadek napięcia. A jeżeli napięcie na rezystorze będzie rosło, to napięcie na cewce będzie malało, ponieważ zgodnie z napięciowym prawem Kirchhoffa, suma napięć cewki i rezystora przez cały czas musi być równa napięciu baterii (U_BAT= U_L+U_R).

Warto rozumieć ten proces właśnie w ten sposób: w każdej chwili przepływający prąd powoduje spadek napięcia na rezystorze o wartości U=I×R, więc na cewce występuje napięcie będące różnicą napięć U_BAT–U_R.

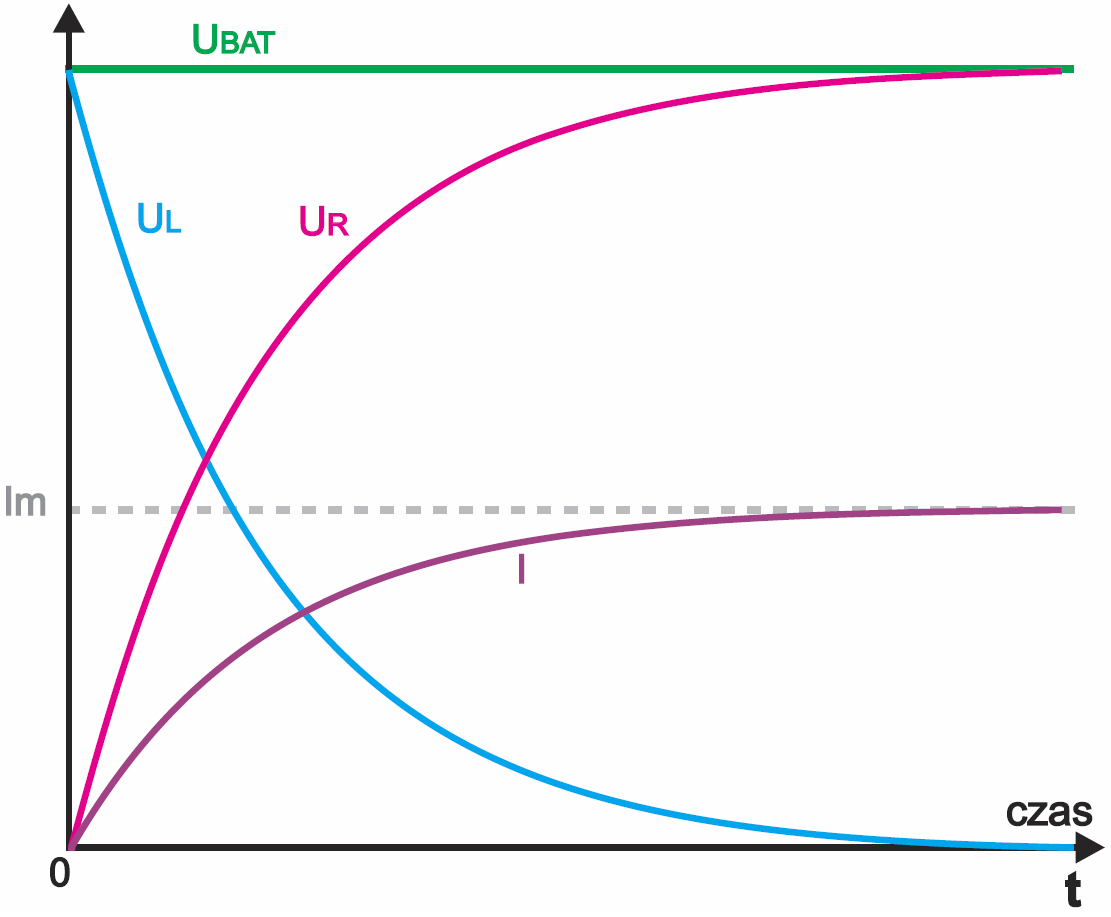
Tymczasem zgodnie z rysunkiem 5 prąd w obwodzie będzie rósł, co spowoduje wzrost napięcia U_R i stopniowe zmniejszanie napięcia U_L. A jeśli napięcie U_L stopniowo będzie maleć, to zgodnie z rysunkiem 7 zmniejszać się będzie też szybkość narastania prądu. W pierwszej chwili po zwarciu wyłącznika S szybkość tego wzrostu będzie największa, jak pokazuje rysunek 4 i 5a, a potem prąd też będzie wzrastał, ale coraz wolniej. Zmiany prądu i napięć na elementach R, L nie będą liniowe, tylko będą wyglądać jak na rysunku 9.

W końcu prąd ustabilizuje się na wartości Im = U_BAT/R, a napięcie na rezystorze osiągnie wartość: Im×R = U_BAT

A to oznacza, że w takim stanie ustalonym przez (idealną) cewkę będzie płynął prąd Im, ale napięcie na niej będzie równe zeru.

Indukcyjność

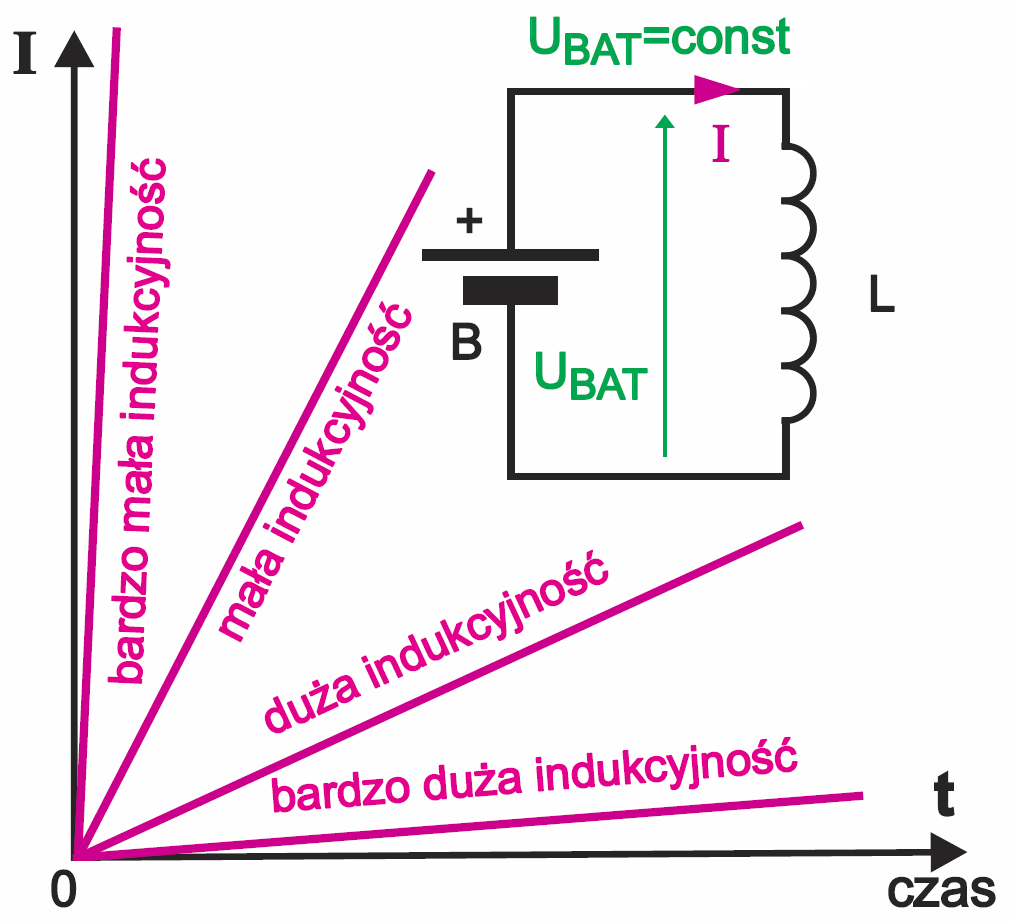
Rysunek 7 wskazał, że czym większe napięcie, tym szybciej narasta prąd w cewce. Takie same wnioski niesie analogia hydrauliczna, która wskazuje dodatkowo, że szybkość narastania prądu będzie też zależeć od właściwości turbiny. Otóż dana turbina może różnić się od innych masą i bezwładnością wirnika. Czym większa masa i bezwładność wirnika, tym turbina jest bardziej „leniwa” i tym wolniej będzie zwiększać swą prędkość i przepływ wody. Tak samo w poszczególnych cewkach przy tym samym napięciu szybkość narastania prądu będzie różna. Będzie zależeć od podstawowego parametru cewki, zwanego indukcyjnością.

Zakoduj sobie w świadomości bardzo ważne, choć wręcz oczywiste stwierdzenie: indukcyjność cewki jest odpowiednikiem bezwładności turbiny w analogii wodnej (w uproszczeniu: odpowiednikiem wielkości i masy koła zamachowego).

Indukcyjność cewki zazwyczaj oznaczamy literą L i wyrażamy w henrach, milihenrach lub mikrohenrach. Nazwa jednostki pochodzi od nazwiska: amerykański naukowiec Joseph Henry (1797–1878) odkrył zjawisko indukcji elektromagnetycznej, niezależnie od Faradaya.

Indukcyjność cewki wskazuje, jak skutecznie cewka przeciwstawia się zmianom wartości prądu. Czym większa indukcyjność cewki, tym wolniej wzrasta prąd, jak pokazuje to rysunek 10.

I oto mamy już elementarne wiadomości o cewce. Ale to jeszcze nie wszystko. Musimy przejść do szczegółów, które dla niektórych początkujących stanowią poważny problem.

Chodzi o zjawisko samoindukcji i wytwarzania przez cewkę napięcia. Zajmiemy się tym w następnym odcinku.

Piotr Górecki