Elektronika (nie tylko) dla informatyków (17) Napięcie samoindukcji

W poprzednim odcinku zajmowaliśmy się zjawiskiem samoindukcji. Zgodnie z obietnicą, w tym wykładzie zajmiemy się zależnościami między napięciem i prądem w cewce.

Przy analizie zwróć szczególną uwagę na podobieństwa i różnice między cewką a kondensatorem. Znajdziesz tu jeszcze jeden argument na poparcie potocznego stwierdzenia, że cewki są odwrotnością kondensatorów.

Napięcie samoindukcji

Mówiliśmy, że cewka „nie lubi” zmian prądu i że reaguje na zmiany prądu wytwarzając „własne” napięcie, tak zwane napięcie samoindukcji. Podstawowa zależność jest tu beznadziejnie prosta: czym większe zmiany prądu, tym wyższe napięcie samoindukcji. I czym większa indukcyjność, tym większe napięcie wywołane zmianą prądu. Natomiast jeśli prąd jest niezmienny, cewka nie wytwarza napięcia samoindukcji. Możemy w uproszczeniu napisać:

U_L = L × (szybkość zmian prądu)

Ściślej biorąc, należałoby to zapisać:

U_L(t) = –L(di/dt)

co w tłumaczeniu z polskiego na nasze znaczy, iż chwilowa wartość powstającego napięcia samoindukcji jest wprost proporcjonalna do indukcyjności i szybkości zmian prądu. Cewka jest „przekorna”, i zawsze biegunowość wytwarzanego przez cewkę napięcia samoindukcji jest taka, by przeciwstawić się zmianom prądu i właśnie tak można najprościej wytłumaczyć obecność znaku minus we wzorze.

Jednak znak minus możemy spokojnie
pominąć i w uproszczeniu zapisać:

U_L(t) = L(di/dt)

W praktyce jeszcze bardziej upraszczamy sytuację. Pomijamy fakt, że chodzi o przyrosty, oznaczone literą delta i zapisujemy tę zależność w jeszcze prostszej postaci:

U_L = LI/t lub częściej spotykanej Ut = LI

W tym miejscu przypomnij sobie kondensator. Tam było podobnie, tylko jakby odwrotnie: prąd był nierozłącznie związany z szybkością zmian napięcia. Teraz w przypadku cewki napięcie samoindukcji jest nierozłącznie związane z szybkością zmian prądu. W przypadku kondensatora mieliśmy dokładny, „naukowy” wzór:

i(t) = C(du/dt)

który w uproszczeniu zapisywaliśmy: a nawet upraszczaliśmy jeszcze bardziej i pisaliśmy: I = CU/t          It = CU

a potem wielokrotnie korzystaliśmy z tego ostatniego wzoru. Teraz okazuje się, że z cewką indukcyjną jest podobnie. Mamy podobne wzory, z których chętnie korzystamy: U×t = L×I oraz I×t = C×U.

Ale wracajmy do fundamentów. Możemy powiedzieć, że w cewce zmiany prądu powodują powstanie napięcia samoindukcji, ale nie należy wyobrażać ich sobie jako „jednokierunkowej” przyczyny i skutku, tylko traktować jako nierozłączną zależność „dwukierunkową”: że obecność na cewce napięcia U_L nierozłącznie wiąże się ze zmianami prądu. Jeśli nie ma zmian prądu, nie ma napięcia samoindukcji. Jeśli jest napięcie samoindukcji, na pewno prąd w cewce rośnie lub maleje.

Chyba bez oporów przyjąłeś wniosek, że przy próbie zmniejszenia prądu, cewka się temu przeciwstawia i wytwarza napięcie samoindukcji, które dodaje się do napięcia zasilającego, by podtrzymać przepływ prądu. A jak jest przy narastaniu prądu?

Oczywisty przykład z wcześniejszych rysunków 4 i 5 (w tym wykładzie), przedstawiający sytuację tuż po zamknięciu obwodu można rozumieć tak: idealna cewka ma rezystancję równą zeru. W obwodzie nie ma żadnych rezystancji. Po dołączeniu napięcia zasilającego, cewka wytwarza napięcie samoindukcji o wartości dokładnie równej wartości napięcia zasilania, tylko o przeciwnej biegunowości. Mamy nie jedno, tylko dwa napięcia o tej samej wartości i przeciwnej biegunowości.

Napięcia te się… znoszą.

Zapewne już zdążyłeś utrwalić sobie prawo Ohma i być może teraz wyda Ci się to niemożliwe, bo jeżeli napięcia się zniosą, to niby dlaczego prąd płynie bez napięcia? Otóż to jest nieprawidłowe podejście – napięcie jest, i to nie jedno, tylko dwa. Ale wartość prądu nie jest tu wyznaczona przez rezystancję, której w tym idealizowanym układzie nie ma. Tutaj to cewka, a dokładniej indukcyjność cewki L, wyznacza wartość, a raczej szybkość narastania prądu, dokładnie według podanej właśnie zależności. Można to rozumieć następująco: bez indukcyjności L i bez rezystancji R prąd natychmiast wzrósłby do nieskończonej wartości. Tu nie pozwala na to cewka. Wytwarza ona napięcie samoindukcji, które odejmuje się od napięcia zasilającego i hamuje wzrost prądu.

Jeszcze raz powtarzam, nie ma tu żadnej magii i cewka niczego nie musi „wiedzieć”. Jeśli zmiany prądu ΔI/Δt byłyby zbyt wolne, wytwarzane napięcie samoindukcji byłoby zbyt małe i niezerowa różnica napięcia zasilającego i napięcia samoindukcji spowodowałaby szybki wzrost prądu, a ten wzrost prądu skutkowałby wzrostem napięcia U_L do potrzebnej wartości. W praktyce wytwarza się więc stan równowagi – prąd będzie rósł z dokładnie taką prędkością, żeby wytwarzane napięcie U_L było dokładnie równe napięciu zasilania.

Mamy tu swego rodzaju sprzężenie zwrotne. Napięcie samoindukcji i szybkość zmian prądu w cewce niejako „pilnują się wzajemnie”, żeby proces przeciwstawiania się zmianom prądu przebiegał prawidłowo przez czas zależny od warunków i dostępnej energii.

To jest rzeczywiście coś zupełnie nowego, a w codziennym życiu niewiele mamy takich zjawisk, a jeśli nawet, to nie wnikamy w ich przyczyny. Dlatego wielu osobom trudno przyswoić sobie i poczuć intuicyjnie właściwości i działanie cewki. Jeżeli i Ty masz z tym kłopot, przeanalizuj dokładnie podany dalej materiał.

Różne punkty widzenia

Wcześniej analizowaliśmy zachowanie obwodów z rysunku 6 (w tym wykładzie). Analogia hydrauliczna podsunęła wniosek, że przyczyną jest napięcie występujące na cewce, a skutkiem jest wzrost prądu. Wróć do rysunku 7 (również w tym wykładzie) i zauważ, że szybkość zmian prądu rzeczywiście jest wprost proporcjonalna do napięcia zasilania. Natomiast rysunek 10 (w tym samym  wykładzie) wskazał, że jest odwrotnie proporcjonalna do indukcyjności L. Możemy to zapisać: szybkość zmian prądu = U/L

Oznacza to, że szybkość zmian prądu w cewce jest wprost proporcjonalna do napięcia U występującego na tej cewce i odwrotnie proporcjonalna do indukcyjności tej cewki. Można też powiedzieć, że indukcyjność wiąże szybkość zmian prądu z napięciem na cewce.

Można byłoby więc stwierdzić, iż podczas ładowania cewki, napięcie na cewce jest przyczyną, a wzrost prądu skutkiem. Ale mówiliśmy też o zjawisku samoindukcji i wtedy podeszliśmy z odwrotnej strony: za przyczynę uznaliśmy zmiany prądu, a za skutek – wytwarzane przez cewkę napięcie samoindukcji.

Zależność: szybkość zmian prądu = U/L należałoby zapisać ściślej: di/dt = U/L a w uproszczeniu: ΔI/Δt = U/L w jeszcze większym uproszczeniu: I/t = U/L czyli zgodnie z wcześniejszym wzorem: Ut = LI

Nie ma tu jednak żadnej sprzeczności. Mamy po prostu dwa spojrzenia na te same zjawiska.

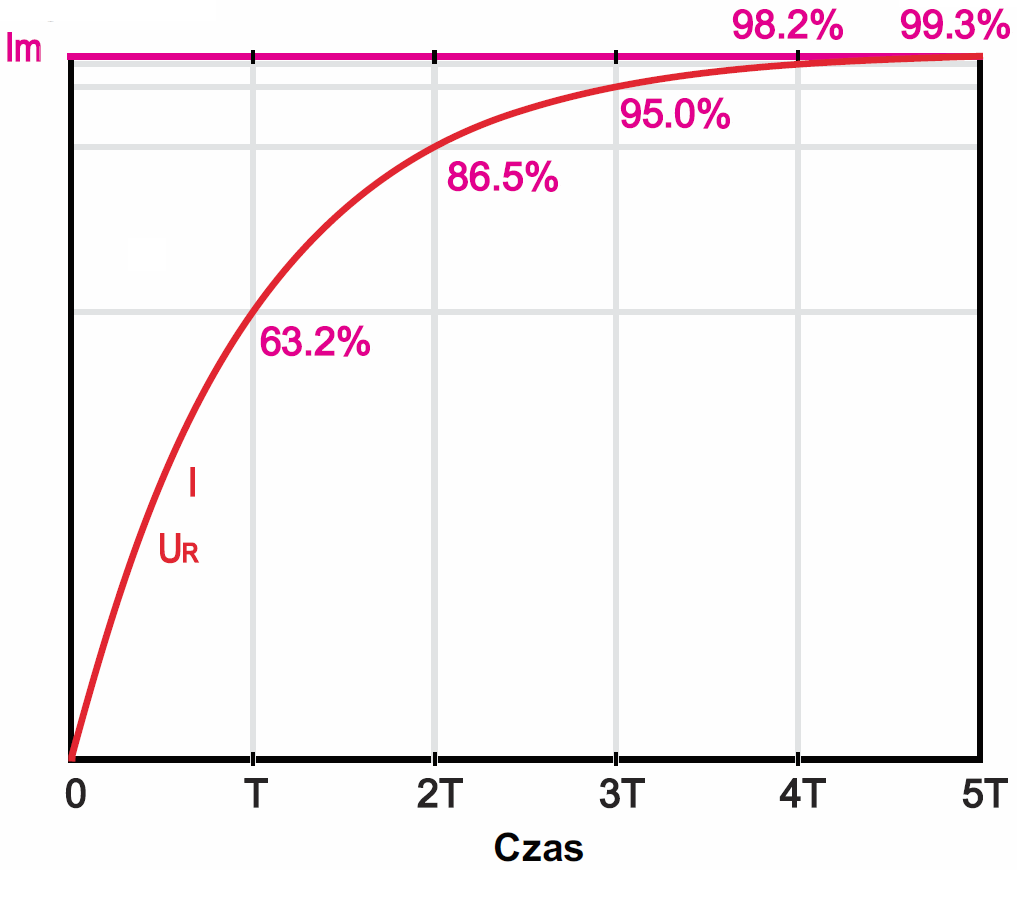
Możemy też spojrzeć inaczej na sytuację z rysunków 6, 8, 9 (w tym wykładzie). Wcześniej traktowaliśmy napięcie na cewce jako przyczynę, a wzrost prądu jako skutek. Teraz popatrzmy z innej strony: w pierwszej chwili po zamknięciu obwodu prąd jest równy zeru, a więc spadek napięcia na rezystancji (U_R = I×R) też jest równy zeru. Ale od tego pierwszego momentu zaczyna wzrastać prąd i na cewce pojawia się napięcie samoindukcji U_L o wartości dokładnie równej napięciu zasilania. Szybkość wzrostu prądu jest dokładnie taka, żeby napięcie było równe napięciu zasilania. Potem jednak ten wzrastający prąd powoduje, że napięcie na rezystorze (U_R=I×R) jest coraz większe. Cewka nadal będzie wytwarzać napięcie samoindukcji U_L, ale napięcie to będzie coraz mniejsze, równe różnicy między napięciem zasilania i napięciem na rezystancji (U_L = U_BAT – U_R). Jeżeli napięcie U_L będzie coraz mniejsze, to zmniejszać się musi wywołująca je szybkość zmian prądu. Prąd będzie narastał coraz wolniej i będzie dążył do wartości Im = U_BAT/R. W szeregowym obwodzie RL przebiegi będą jak na rysunku 9 (w tym wykładzie). Teoretycznie prąd osiągnie wartość Im po czasie nieskończenie długim, ale w praktyce nie jest tak źle – nie musimy obawiać się tej nieskończoności.

Otóż analogicznie jak w obwodzie szeregowym RC, możemy tu mówić o stałej czasowej obwodu (T = L/R) czyli czasie, po którym prąd osiągnie 63% maksymalnej wartości. Jak pokazuje rysunek 1, prąd i napięcie na rezystorze osiągną wartość 99,3% Im już po stosunkowo krótkim czasie 5T.

Moglibyśmy zastanawiać się nad tym, dlaczego zmniejszenie rezystancji powoduje zwiększenie stałej czasowej (T = L/R) i jakie to ma skutki. To rzeczywiście wymyka się intuicji. Jednak w praktyce nie wykorzystujemy obwodów czasowych LR, dlatego nie będziemy się wgłębiać w takie analizy. A tak przy okazji: czy zależność szybkość zmian prądu = U/L przypomina Ci choć trochę prawo Ohma i wzór I = U/R?

Owszem, można uznać, że jakieś podobieństwo istnieje, niemniej na pewno indukcyjność, choć przeciwstawia się zmianom prądu, nie jest opornością taką jak rezystancja.

Zwróć też uwagę na inny szczegół. Otóż w obwodzie z rysunków 4, 7 (w tym wykładzie) teoretycznie prąd będzie liniowo rósł w nieskończoność. W praktyce nie wzrośnie do nieskończoności, ale może osiągnąć bardzo dużą wartość. Powróćmy do analogii hydraulicznej – duży i wciąż rosnący przepływ wody będzie zwiększał prędkość obrotową turbiny i nietrudno się domyślić, że w końcu dojdzie do jakiejś awarii. Zapewne do „jakiejś awarii” dojdzie też w rzeczywistej cewce. I to jest bardzo ważna sprawa, którą zajmiemy się w następnym odcinku.

A na razie utrwal sobie podstawową, dziecinnie prostą zasadę działania cewki indukcyjnej: cewka nie lubi zmian prądu i na zmiany prądu reaguje wytworzeniem napięcia samoindukcji. Biegunowość wytwarzanego napięcia samoindukcji zależy od tego, czy prąd wzrasta, czy maleje. Wartość napięcia na cewce jest nierozłącznie związana z szybkością zmian płynącego przez nią prądu: czym szybsze zmiany prądu, tym wyższe napięcie samoindukcji.

Piotr Górecki