Elektronika (nie tylko) dla informatyków (29) Transformator rzeczywisty – Straty i ograniczenia

W poprzednim odcinku przyglądaliśmy się transformatorowi w stanie jałowym oraz transformatorowi obciążonemu rezystancją. Nasze rozważania dotyczyły transformatora idealnego W tej części przyjrzymy się różnym ograniczeniom, które występują w rzeczywistym transformatorze.

Transformator rzeczywisty – straty w żelazie i w miedzi

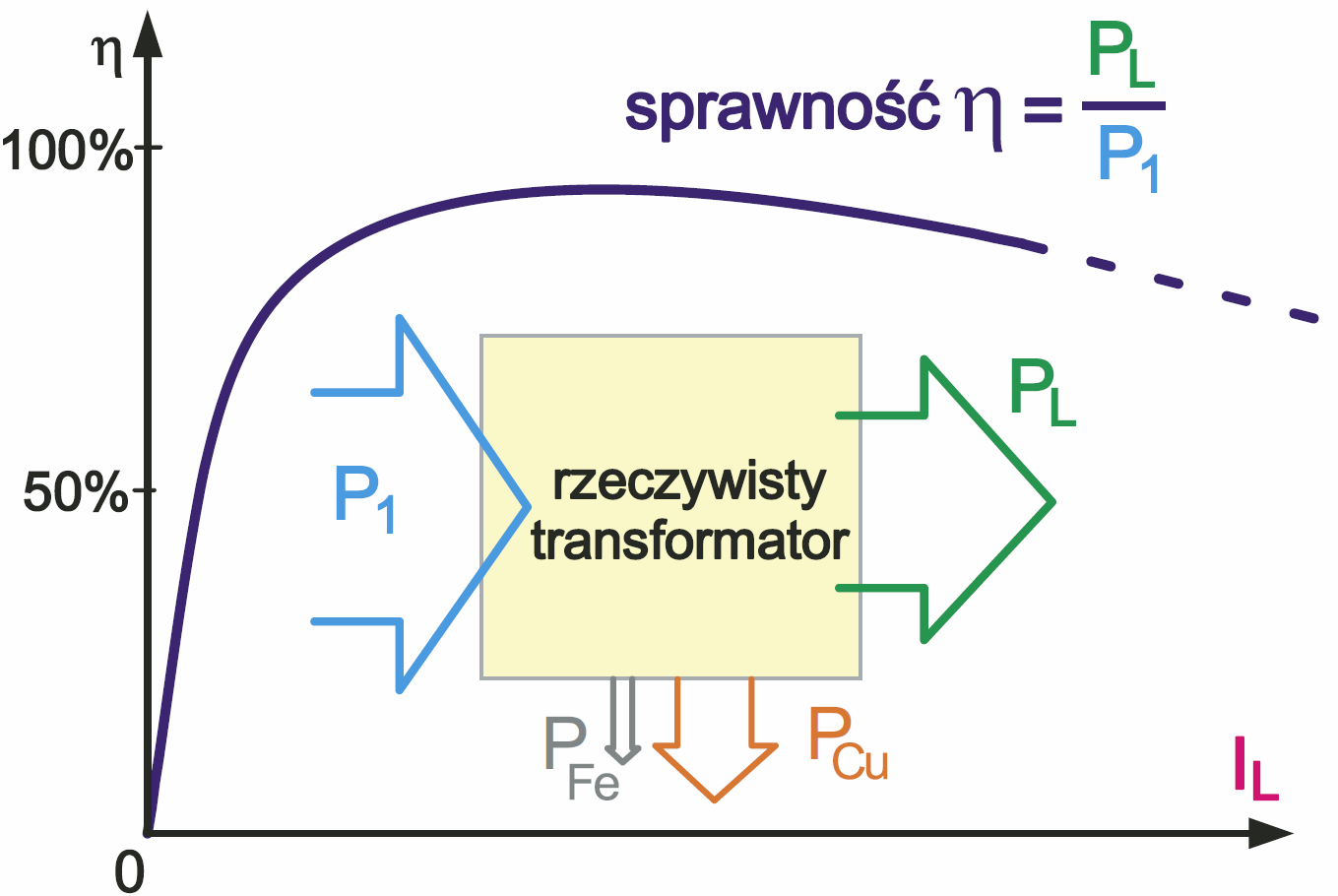
We wcześniejszych rozważaniach całkowicie pominęliśmy problem strat. Przy takim założeniu okazało się, że transformator idealny, nawet bardzo mały, może przenieść dowolnie dużą moc. Tymczasem rzeczywiste transformatory niewątpliwie mają ograniczoną moc. Wystarczy obejrzeć popularne transformatory sieciowe, by przekonać się, że moc transformatora jest tym większa, im większy jest rdzeń. W rzeczywistych transformatorach występują straty, to znaczy, że nie cała energia pobrana ze źródła zasilania zostaje dostarczona do obciążenia. Część energii po drodze zamienia się na ciepło. Miarą jest tu sprawność energetyczna transformatora, która jest stosunkiem mocy dostarczonej do obciążenia (P_L) i mocy pobieranej ze źródła (P₁):

η = P_L/ P₁ = U_L×I_L / U₁×I₁

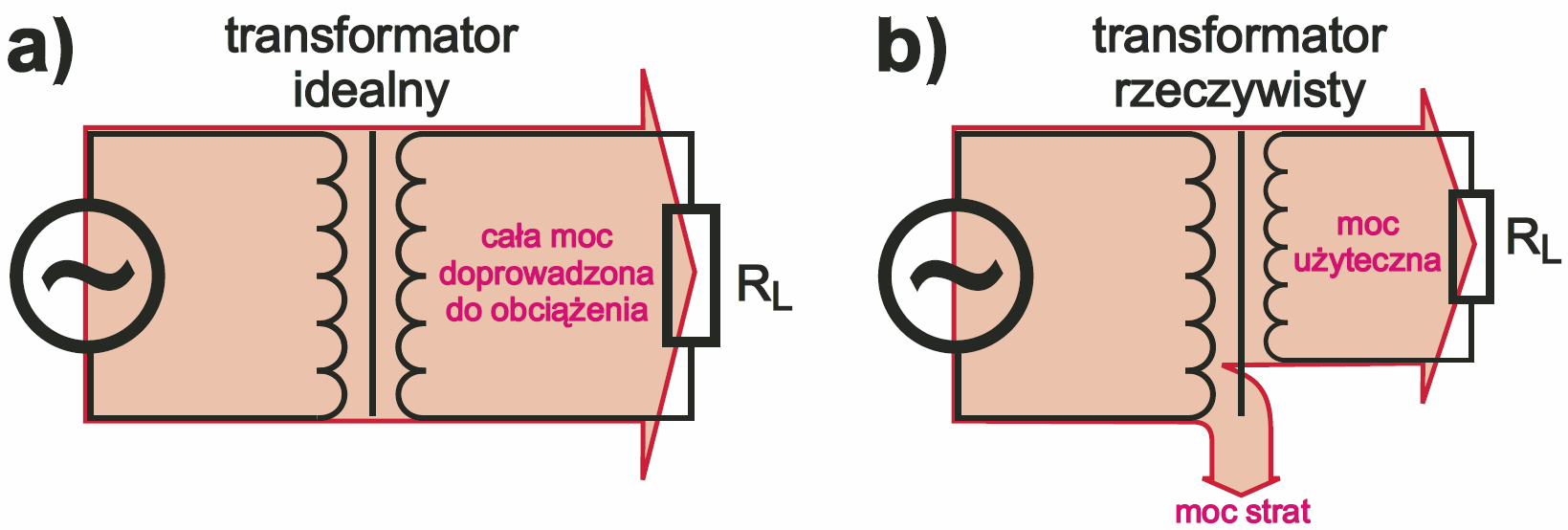
W przypadku idealnym sprawność byłaby równa 1 (100%) – wtedy cała energia ze źródła zasilania byłaby przekazywana przez transformator do obciążenia, co ilustruje rysunek 1a. W rzeczywistości sprawność jest zawsze mniejsza od 100%, w praktyce około 70…95%, jak pokazuje rysunek 1b. Sprawność energetyczna to ważny parametr, ale nas interesuje bardziej, od czego zależy maksymalna moc, przenoszona przez rzeczywisty transformator?

Na pewno ta maksymalna moc jest jakoś związana ze stratami. W transformatorach mamy dwie główne przyczyny strat, dlatego często mówimy o stratach:

– w miedzi,

– w żelazie.

Straty w miedzi to prostu straty cieplne w rezystancji miedzianych uzwojeń. Prąd, płynąc przez te uzwojenia, powoduje wydzielanie się mocy strat P = I²R. Jak widać, straty miedzi rosną wraz ze wzrostem prądu, i to nie liniowo, tylko proporcjonalnie do drugiej potęgi prądu, czyli z kwadratem prądu. Przykładowo dziesięciokrotny wzrost prądu powoduje stukrotne zwiększenie strat w miedzi.

Straty w żelazie – to nie do końca ścisłe określenie bierze się stąd, że dawniej wykorzystywano głównie transformatory budowane w oparciu o rdzenie, których głównym składnikiem było żelazo. Najogólniej biorąc, na straty w żelazie składają się dwa zjawiska. Pierwsza przyczyna: podczas pracy transformatora przepływający prąd przemienny powoduje, że rdzeń jest na przemian magnesowany, rozmagnesowywany, magnesowany w przeciwnym kierunku, rozmagnesowywany i tak dalej. Występuje przy tym tzw. zjawisko histerezy i każdy cykl takiego przemagnesowywania wiąże się z zamianą niewielkiej porcji energii na ciepło.

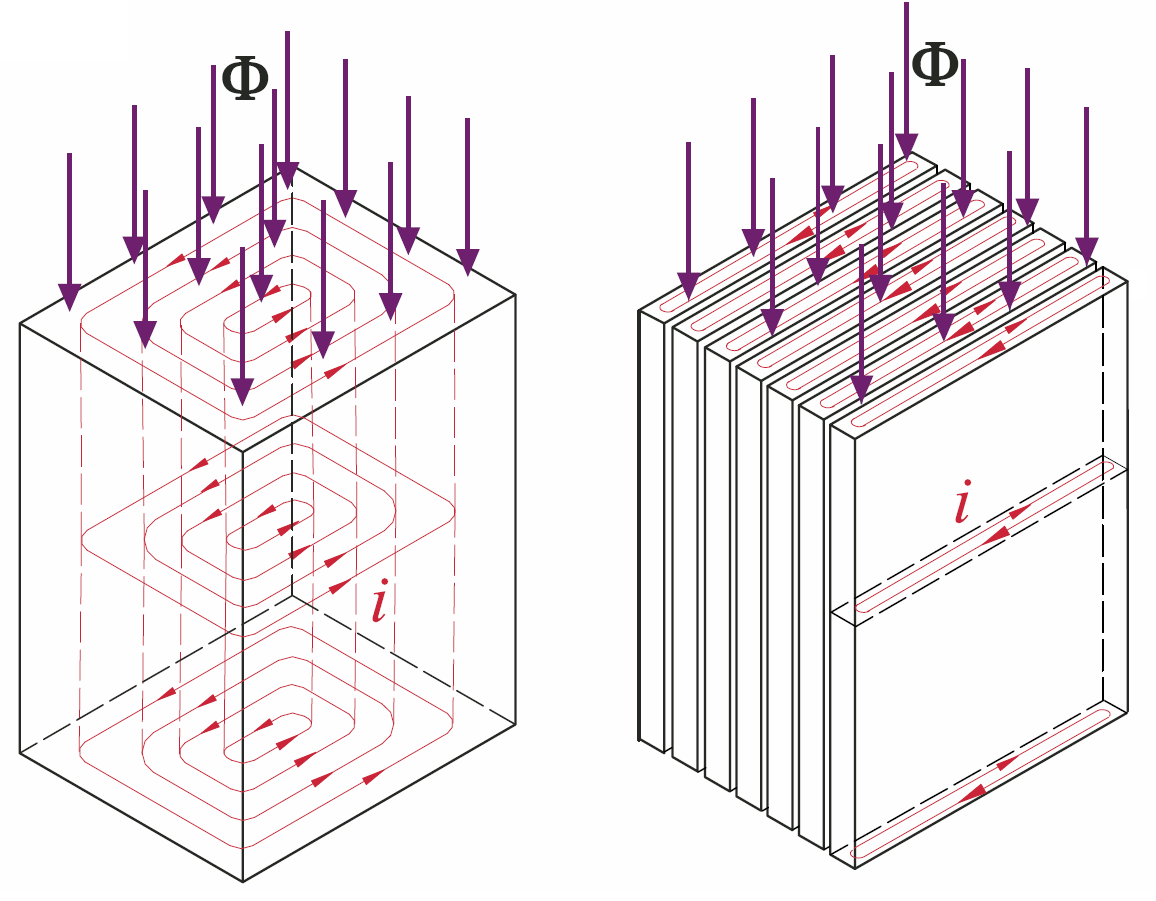
Druga przyczyna strat w żelazie wynika ze zjawiska, które jest podstawą działania transformatora. Mianowicie zmienny strumień magnetyczny indukuje napięcie nie tylko w każdym zwoju, ale we wszystkich przewodzących częściach, a więc także w rdzeniu. Tak indukowane napięcia powodują przepływ prądów, zwanych prądami wirowymi (eddy current). Prądy te, płynąc przez rezystancję rdzenia, powodują straty i wydzielanie ciepła (tzw. straty wiroprądowe). Aby zminimalizować ten efekt, należałoby zastosować rdzeń bardzo słabo przewodzący prąd. Bardzo słabo przewodzą prąd tzw. rdzenie ferrytowe przedstawione na fotografii 2.

Natomiast w transformatorach sieciowych zaprezentowanych na fotografii 3 rdzeń jest stalowy i generalnie dość dobrze przewodzi prąd. Wtedy dla zmniejszenia prądów wirowych wykonuje się rdzeń…

– z cienkich arkuszy lakierowanej blachy

– z dodatkiem krzemu, który zwiększa rezystancję blachy.

Obecność krzemu i podzielenie rdzenia na wąskie, wzajemnie izolowane blaszki poważnie zmniejsza problem prądów wirowych, powstających pod wpływem zmian strumienia, co jest w uproszczeniu pokazane na rysunku 4.

Trzeba też bardzo mocno podkreślić, że w klasycznych transformatorach sieciowych 50 Hz straty mocy w żelazie, czyli w rdzeniu, są stosunkowo niewielkie i co ważne: stałe, niezależne od obciążenia. Straty w żelazie zależą od napięcia zasilającego, a dokładniej od strumienia, oraz od częstotliwości. Ponieważ w transformatorach sieciowych 230 V i napięcie zasilające, i strumień, i częstotliwość, mają ustaloną wielkość (porównaj rysunek 3 w poprzednim odcinku), wartość strat w żelazie jest taka sama w stanie jałowym, jak i pod obciążeniem.

Inaczej jest ze stratami w miedzi – tu w grę wchodzi rezystancja miedzianego drutu i wydzielane w niej tzw. ciepło Joule’a o mocy określonej wzorem P=RI². W stanie jałowym prąd płynie tylko przez uzwojenie pierwotne i jest to jedynie prąd magnesujący o niewielkiej wartości. Prąd ten, płynąc przez niezbyt dużą rezystancję uzwojenia pierwotnego, powoduje wydzielanie się mocy strat, która jest bardzo mała, mniejsza od mocy strat w żelazie.

Natomiast gdy w obciążonym transformatorze przez oba uzwojenia zaczynają płynąć większe prądy, powodują one coraz większe straty mocy w rezystancji obu uzwojeń. Nie musimy analizować szczegółowo strat w obu uzwojeniach, ważne jest tylko, że straty w miedzi są wprost proporcjonalne do kwadratu prądu (P=I²). To znaczy, że gdy na przykład prąd wzrośnie czterdziestokrotnie, co jest realne, to straty w miedzi wzrosną tysiąc sześćset razy! Co ważne, w spoczynku straty w miedzi są mniejsze od strat w żelazie, ale przy znacznym obciążeniu, szybko rosnące straty w miedzi stają się wielokrotnie większe i to one stanowią główny problem, zwłaszcza w transformatorach sieciowych.

Ograniczenia mocy

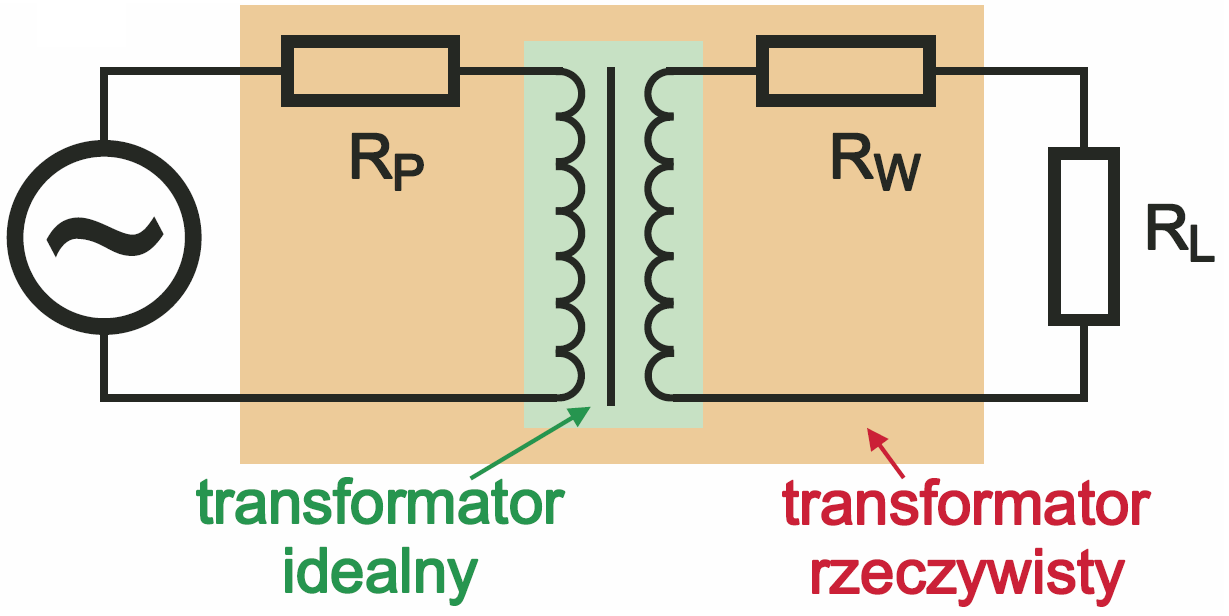
Wyjaśniliśmy z grubsza problem strat w żelazie i miedzi, ale niewiele nas to przybliżyło do odpowiedzi na pytanie o moc maksymalną transformatora. Wcześniejsze rozważania podpowiadają, iż główną przyczyną ograniczeń są straty w miedzi… Dlatego narysujmy schemat zastępczy transformatora z dwiema rezystancjami uzwojeń R_P i R_W, jak na rysunku 5. Pomijamy tu straty w żelazie, które są niewielkie i niezmienne.

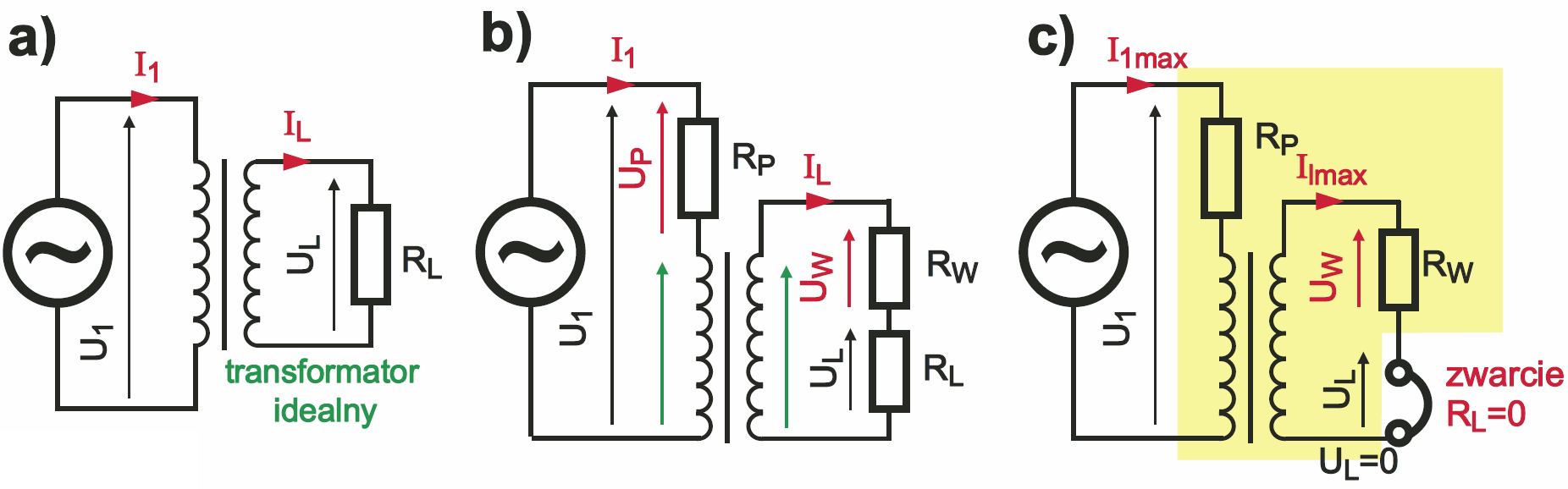
Gdybyśmy chcieli je zobrazować, dorysowalibyśmy reprezentujący je rezystor „na wejściu”, równolegle do źródła zasilania. Zaniedbajmy też na razie straty, wynikające z przepływu prądu magnesującego przez rezystancję uzwojenia pierwotnego, bo mają one znikomo małą wartość. Skupmy się na stratach w miedzi, związanych z przepływem prądu obciążenia: to oczywiste, że przy wzroście prądu wyjściowego I_L, wzrastał będzie też prąd I₁. Te wzrastające prądy będą powodować niekorzystne spadki napięć na rezystancjach uzwojeń, co jest zobrazowane na rysunku 6.

W rzeczywistym transformatorze prądy I₁ i I_L nie mogą wzrastać nieograniczenie. Największą dla danego transformatora wartość (I_1max, I_Lmax) osiągną wtedy, gdy R_L=0, czyli gdy uzwojenie wtórne zostanie zwarte – rysunek 6c. Wtedy ze źródła zasilania o danym napięciu U₁ transformator będzie pobierał maksymalną moc P = U₁×I_1max. Owszem, można tu mówić o mocy maksymalnej transformatora, gdy cała moc pobierana ze źródła zamienia się na ciepło: znikoma jej część w postaci strat w żelazie (co pominęliśmy na rysunku 6c), zdecydowana większość jako straty w rezystancji miedzianych uzwojeń. Przy prądzie I_Lmax, czyli przy zwarciu wyjścia, napięcie wyjściowe U_L jest równe zeru, a to znaczy, że przy zwarciu moc wyjściowa, czyli moc dostarczana do obciążenia… jest równa zeru. A przecież nas interesuje moc użyteczna, czyli moc przenoszona przez transformator do obciążenia.

Moc maksymalna i sprawność

Aby zgłębić temat maksymalnej mocy użytecznej, moglibyśmy badać zależność sprawności od prądu wyjściowego, uwzględniając straty w żelazie i miedzi. Okazałoby się, że przy wzroście prądu sprawność najpierw szybko rośnie, a potem zaczyna się obniżać, jak pokazuje rysunek 7, a wreszcie przy prądzie zwarcia sprawność osiągnęłaby wartość zero. Takie rozważania nie byłyby jednak dobrym tropem.

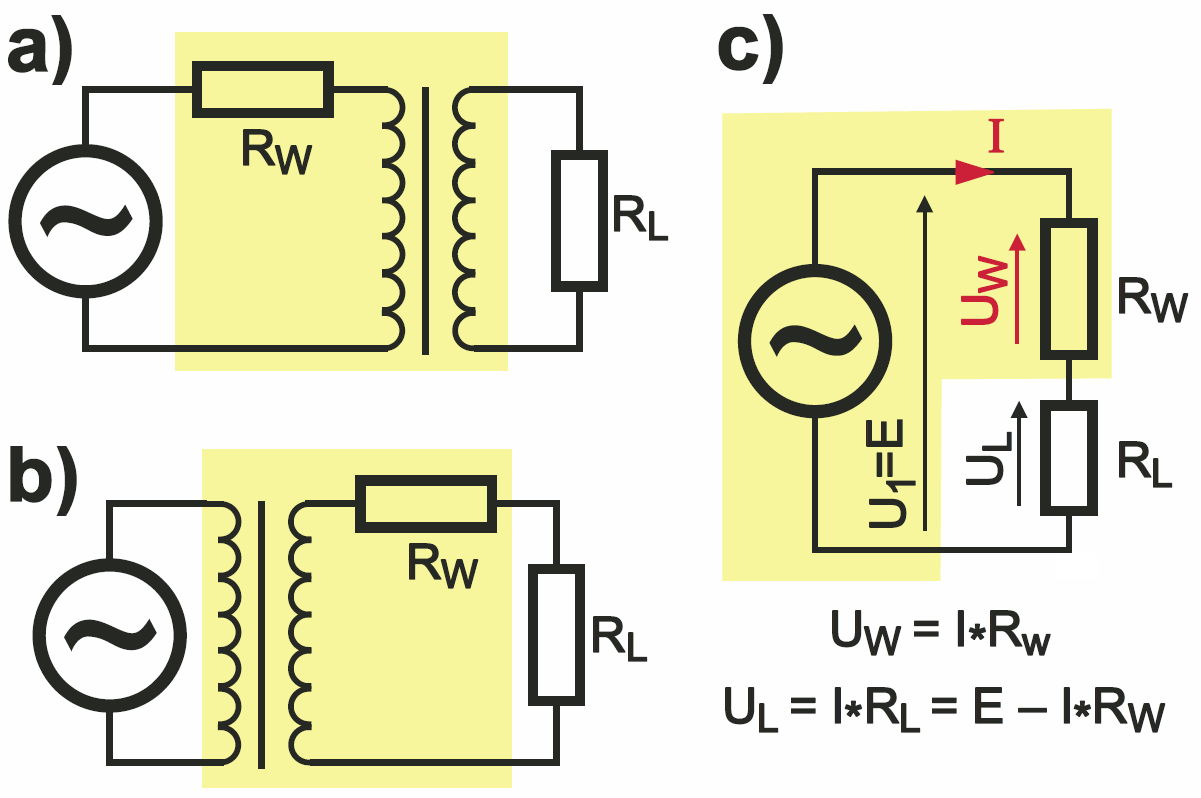
Zastanówmy się raczej nad mocą dostarczaną do obciążenia R_L. Zauważmy, że prądy I₁, I_L są ze sobą nierozłącznie związane przekładnią transformatora. Dla ułatwienia analizy możemy więc uprościć układ z rysunku 5 do postaci jak na rysunku 8a lub rysunku 8b, gdzie rezystancja R_W reprezentuje wypadkową oporność obu uzwojeń transformatora. Aby jeszcze bardziej uprościć zagadnienie: załóżmy, że transformator ma przekładnię równą jedności – wtedy schemat zastępczy możemy uprościć jeszcze bardziej, do postaci z rysunku 8c. I teraz możemy zrobić następny ważny krok.

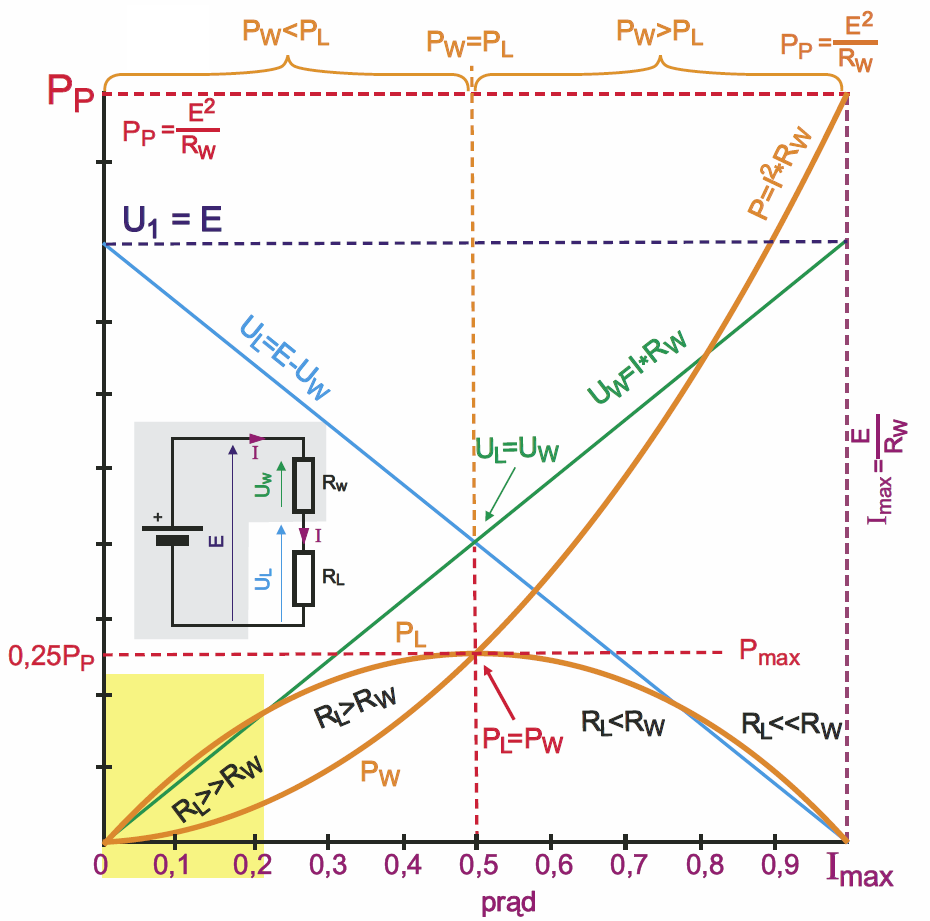
Ze szkolnych podręczników fizyki wiadomo, że źródło zasilania dostarczy do obciążenia maksymalną moc P_max, gdy rezystancja obciążenia R_L będzie równa rezystancji źródła R_W (R_L=R_W). A gdy rezystancja obciążenia jest mniejsza i większa od R_W, wtedy moc dostarczana do obciążenia jest mniejsza od tej mocy maksymalnej P_max. Zależność tę przedstawia rysunek 9. Jest to wykres napięć i mocy przy zmianach prądu, wywołanych zmianami rezystancji R_L. Zakładamy, że rezystancja R_W danego źródła (transformatora) jest niezmienna. Gdy R_L maleje, wtedy rośnie prąd I. Ze wzrostem prądu liniowo rośnie też napięcie na R_W (U_W=I×R_W), a to oznacza, że napięcie na R_L będące różnicą E–U_W zmniejsza się (liniowo). Pokazują to proste, zielona i niebieska. Wzrost prądu i wzrost napięcia na R_W powodują wzrost mocy wydzielanej w rezystancji, ale nie liniowo, tylko zgodnie z funkcją kwadratową: P_W = I×U_W = I×I×R_W = I²R_W

Przebieg krzywej P_W jest taki, jak funkcji y=x² dla x należącego do przedziału 0, 1. Jest to zgodne, a przynajmniej niesprzeczne z intuicją. Intuicja mniej natomiast pomoże przy określeniu mocy P_L, wydzielanej w obciążeniu R_L. Można jednak wyprowadzić matematyczną zależność:

P_L = I×U_L oraz U_L = E – IR_W          podstawiamy:          P_L = I×(E – IR_W) = I×E – I²R_W          lub inaczej:          P_L = – I²R_W + I×E

Ponieważ prąd I to nasza zmienna, a R_W i E są niezmienne i znane, więc podstawiając R_W=a, E=b, mamy znaną matematyczną funkcję: y = – ax² + bx

Należałoby zbadać taką funkcję kwadratową. Dla wartości x z przedziału 0…1 ma ona przebieg jak krzywa P_L na rysunku 9. Na pierwszy rzut oka może się wydać dziwne, dlaczego osiąga ona wartość zero przy prądzie maksymalnym (I_max=E/R_W). Ale nic w tym dziwnego. Zwiększanie prądu oznacza, że rezystancja R_L dąży do zera. Prąd wprawdzie jest duży, ale przecież napięcie U_L na R_L dąży do zera, dlatego moc P_L też dąży do zera i osiąga zero przy R_L=0 czyli przy zwarciu źródła zasilania (porównaj rysunek 6c). W rezystancji R_W, czyli w (zwartym) transformatorze wydziela się wtedy największa moc P_P=E²/R_W. Natomiast maksymalna moc w obciążeniu R_L wydziela się, gdy R_L=R_W. Wtedy P_L=P_W=P_max=E²/(4RL)=0,25P_P.

Tu mniej zorientowany elektronik gotowy jest uznać, że katalogowa moc transformatora to właśnie moc maksymalna P_max, jaką może on oddać przy R_L=R_W. Prawda jest inna. Transformatory normalnie pracują w warunkach, gdy R_L>R_W, a zwykle R_L>>R_W, a to oznacza, że przenoszona moc jest mniejsza od pokazanej na rysunku 9 mocy P_max, często dużo mniejsza.

Problem w tym, że gdy R_L=R_W, wtedy w rezystancji R_W, czyli w uzwojeniach transformatora, wydzieli się tyle samo mocy, co w obciążeniu, czyli sprawność wynosi 50% (pomijając niewielkie straty w żelazie). Oznacza to marnowanie połowy energii. A przecież chcielibyśmy, żeby sprawność była wyższa.

Ale problem polega nie tylko na marnowaniu energii i zwiększeniu kosztów, bo to od biedy moglibyśmy zaakceptować. Otóż moc strat, wydzielająca się w postaci ciepła, podgrzewa transformator. I właśnie tu leży główny problem.

Co ciekawe, tylko w najmniejszych transformatorach sieciowych o mocy 2…6 W możliwa byłaby praca przy R_L=R_W. W niektórych takich transformatorach małej mocy celowo zwiększa się rezystancję R_W, by uzyskać tzw. transformatory zwarciobezpieczne, czyli takie, w których po 4 godzinach zwarcia uzwojenia wtórnego, temperatura uzwojeń nie przekroczy określonej granicy (zwykle +130° C).

Natomiast w transformatorach większej mocy praca w sytuacji, gdy R_L=R_W, jest możliwa, ale tylko przez krótki czas. Wtedy transformator ma sprawność nieco poniżej 50%, co oznacza, iż tylko połowa mocy jest przekazywana do obciążenia, a druga połowa wydziela się w postaci ciepła i silnie podgrzewa uzwojenia i cały transformator. Sprawność energetyczna dużych transformatorów o mocach powyżej 100 W zwykle jest lepsza niż 90%, a w transformatorach mniejszych, o mocach od kilku do kilkudziesięciu watów, też zwykle nie jest gorsza od 80%. Przy większych transformatorach sprawność rzędu 50% oznaczałaby nie tylko fatalne marnotrawstwo energii, ale też konieczność bardzo intensywnego chłodzenia uzwojeń, co z uwagi na budowę transformatora, wcale nie jest takie proste.

Zapamiętaj więc ważny wniosek, że ogromnej większości transformatorów nie można obciążać mocą P_max, wyznaczoną w sumie przez zastępczą rezystancję wewnętrzną R_W. Nominalna moc transformatorów P_NOM, czyli największa moc użyteczna, podawana przez producentów w katalogach, jest zwykle dużo niższa od pokazanej na rysunku 9 mocy P_max. Na tyle niższa, żeby przy tej mocy nominalnej straty transformatora nie przekraczały kilku, najwyżej kilkunastu procent mocy pobieranej ze źródła zasilania, jak pokazuje to wcześniejszy rysunek 1b. Dlatego też na rysunku 7 linią ciągłą zaznaczona jest sprawność dla prądów od zera do katalogowego prądu nominalnego I_NOM, którego wartość jest kilkakrotnie mniejsza od maksymalnego prądu zwarciowego I_max, natomiast linią przerywaną dla prądów większych od I_NOM.

Choć więc nominalna moc użyteczna transformatora (P_NOM) jest ściśle związana ze sprawnością, jednak głównym ograniczeniem okazuje się wzrost temperatury. Przyjrzyjmy się tej kwestii nieco bliżej.

Moc maksymalna i wzrost temperatury

Dopiero teraz doszliśmy do praktycznego oblicza problemu maksymalnej mocy użytecznej transformatora. Otóż nie możemy tak po prostu stwierdzić: a co nas obchodzi wzrost temperatury transformatora? Niech się grzeje!

Jednym z powodów jest to, że materiał magnetyczny rdzenia przy podgrzaniu do zbyt wysokiej temperatury… przestanie być materiałem magnetycznym, co przy pracującym transformatorze spowodowałoby katastrofalny spadek indukcyjności L, reaktancji X_L, a zatem wzrost prądu i strat cieplnych. Tu przypomnę podręcznikową, szkolną informację, że materiały magnetyczne mają istotny w tym przypadku parametr, tzw. punkt Curie. Punkt Curie to temperatura, w której materiał ferromagnetyczny gwałtownie traci swoje właściwości magnetyczne (i staje się paramagnetykiem). W praktyce zjawisko to nie jest kluczowym ograniczeniem w transformatorach, ponieważ temperatura Curie dla blachy stosowanej na rdzenie wynosi kilkaset stopni. Gdyby brać pod uwagę tylko punkt Curie, rdzeń pracującego transformatora mógłby mieć temperaturę na przykład +300° C lub nawet większą.

Praktyczne ograniczenie leży gdzie indziej. Pamiętamy przecież, że większość strat występuje w miedzi, czyli w uzwojeniach, wykonanych z izolowanego drutu miedzianego. Źródłem ciepła i najgorętszym składnikiem jest miedziany drut uzwojeń. Izolacja drutu może być wykonana z różnych materiałów. Ponieważ zazwyczaj zależy nam na tym, żeby rezystancja drutu była możliwe mała, więc chcielibyśmy, żeby drut był możliwe gruby, a izolacja możliwe cienka, by nie zajmowała cennego miejsca. Między innymi dlatego uzwojenia transformatorów powszechnie wykonuje się z drutu powleczonego cieniutką warstewką izolacyjnego lakieru – emalii. Fotografia 10 pokazuje taki emaliowowany drut nawojowy z częściowo usuniętą (zeskrobaną) emalią. Jak widać, taka emaliowa izolacja jest bardzo cienka. Ma też ograniczoną odporność na temperaturę. Przez długie lata wykorzystywano lakiery izolacyjne, które mogły pracować w temperaturach nie wyższych niż +130° C. Potem wprawdzie wprowadzono lakiery i inne substancje izolacyjne, mogące pracować w temperaturach do +180° C, a nawet jeszcze wyższych (np. teflon), ale w grę wchodzą też koszty wytwarzania drutu nawojowego w specjalnej izolacji. Problem dotyczy również innych elementów izolacyjnych, np. karkasu, czyli szpulki, na której nawinięte są uzwojenia. Także z innych względów nie dopuszcza się, żeby temperatura pracującego transformatora była zbyt wysoka. Przecież ciepło wydzielane w uzwojeniach podgrzewa nie tylko karkas i rdzeń, ale też całe urządzenie, w którym zamontowany jest transformator. Choćby ze względów bezpieczeństwa trudno sobie wyobrazić domowy sprzęt elektroniczny, gdzie pracujący transformator miały temperaturę kilkuset stopni.

No i właśnie omówiliśmy kluczowe ograniczenie: okazuje się nim wynikająca z mocy strat maksymalna temperatura uzwojeń i w ogóle maksymalna temperatura transformatora i urządzenia.

Tu warto wspomnieć, że nieprzypadkowo w dużych transformatorach energetycznych stosuje się olej transformatorowy. Nie służy on jako materiał izolujący, tylko właśnie jako czynnik chłodzący. Olej szybciej niż powietrze odbiera ciepło wytwarzane w uzwojeniu i przekazuje je do otoczenia. Natomiast w klasycznych transformatorach powszechnego użytku ciepło wytwarzane w uzwojeniach musi się z nich wydostać i rozproszyć do otoczenia „w zwykły sposób”, co ogranicza moc.

Można też jeszcze raz wspomnieć o transformatorach zwarciobezpiecznych. Otóż niektóre transformatory o małej mocy, rzędu kilku watów, celowo są projektowane tak, żeby miały dużą rezystancję uzwojeń. Parametry, w szczególności rezystancja uzwojeń, są dobrane tak, że nawet w przypadku zwarcia wyjścia całkowita moc strat w sytuacji z rysunku 6c nie spowoduje wzrostu temperatury uzwojeń powyżej granicy wyznaczonej przez emaliową izolację drutu. Ale to dotyczy tylko najmniejszych transformatorów sieciowych o mocach nominalnych 2…6 W, i to nie wszystkich, tylko niektórych. Natomiast pozostałe małe transformatory mają moc nominalną wyznaczoną w sumie przez maksymalną temperaturę uzwojeń, a przy zwarciu wyjścia według rysunku 6a nastąpi ich przegrzanie i uszkodzenie.

Może teraz uważasz, iż omówiliśmy już wszystkie ograniczenia i że zaraz podam Ci wzór na maksymalną moc użyteczną transformatora. Niestety nie! Wzoru na moc maksymalną transformatora… nie ma. Na razie zbadaliśmy, na ile ograniczeniem są straty w miedzi i sprawność. Ale nadal szukamy odpowiedzi na pytanie, dlaczego i jak moc transformatora związana jest z wielkością rdzenia. I nadal nie widzimy tego związku. A przecież codzienna praktyka świadczy, że taki związek jest. Sprawa nie jest prosta, ale teraz jesteśmy już o krok od uchwycenia kluczowych zależności. Zajmiemy się tym w następnym odcinku.

Piotr Górecki