Elektronika (nie tylko) dla informatyków (13) Kondensator w roli filtru

W ostatnim wykładzie analizowaliśmy pracę kondensatora w roli źródła energii. Teraz zajmiemy się drugim ważnym powodem tak powszechnego wykorzystywania kondensatorów.

Kondensator jako filtr

Kondensatory pozwalają oddzielać przebiegi zmienne od napięć i prądów stałych oraz rozdzielać przebiegi o różnych częstotliwościach. W sumie wszystko polega na cyklicznym ładowaniu i rozładowywaniu kondensatora i zależy od szybkości zmian napięcia, ale przy analizie zwracamy uwagę głównie na reaktancję.

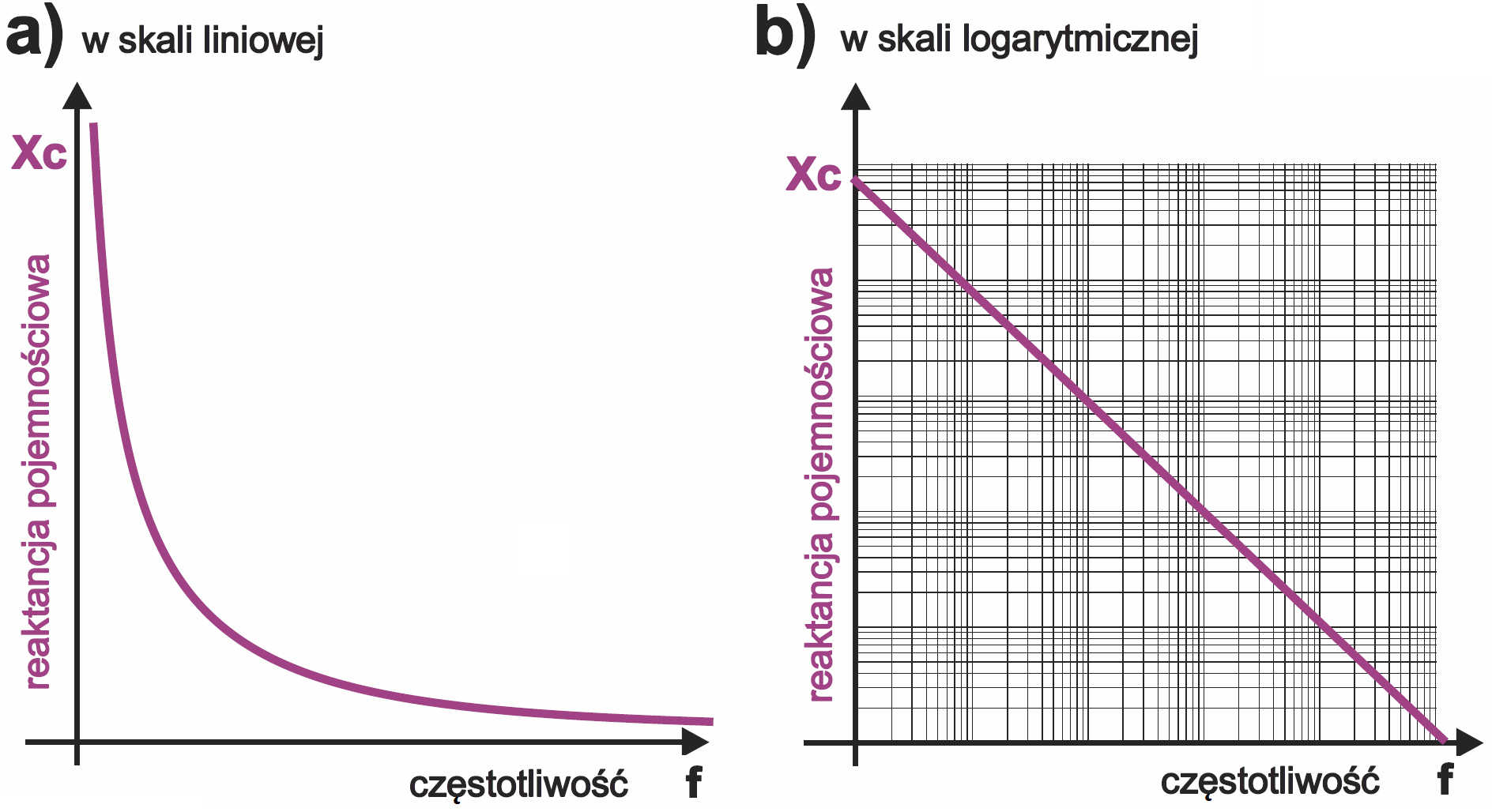
Wiesz dobrze, że dla przebiegów sinusoidalnie zmiennych kondensator przedstawia sobą oporność – reaktancję pojemnościową: X_C = 1 / 2 πfC

Czym większa częstotliwość f, tym mniejsza jest reaktancja pojemnościowa – patrz rysunek 1a. Jeśli przedstawimy częstotliwość i reaktancję w skali logarytmicznej, to wykresem będzie piękna linia prosta, jak na rysunku 2b. Właśnie z uwagi na zależność reaktancji od częstotliwości kondensatory pełnią kluczową rolę w mniej lub bardziej skomplikowanych filtrach.

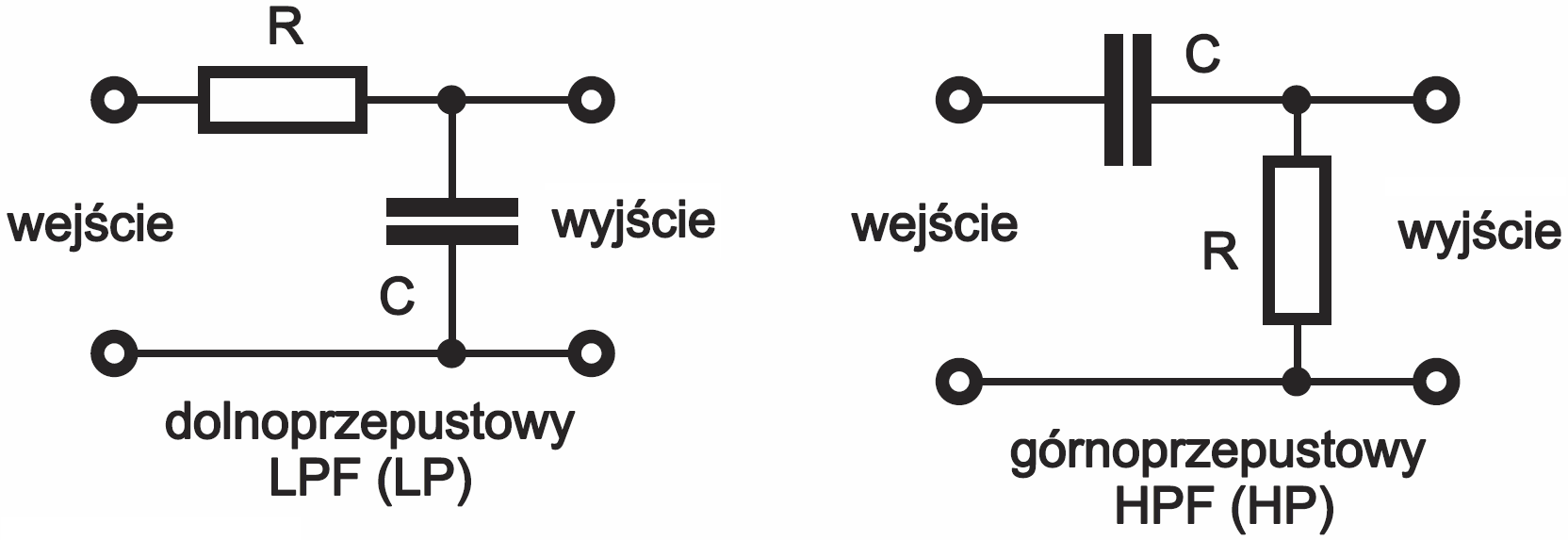
W praktyce bardzo często mamy do czynienia z obwodami RC, które są najprostszymi filtrami – rysunek 2 pokazuje filtr dolnoprzepustowy (LPF – LowPass Filter) i górnoprzepustowy (HPF – HighPass Filter).

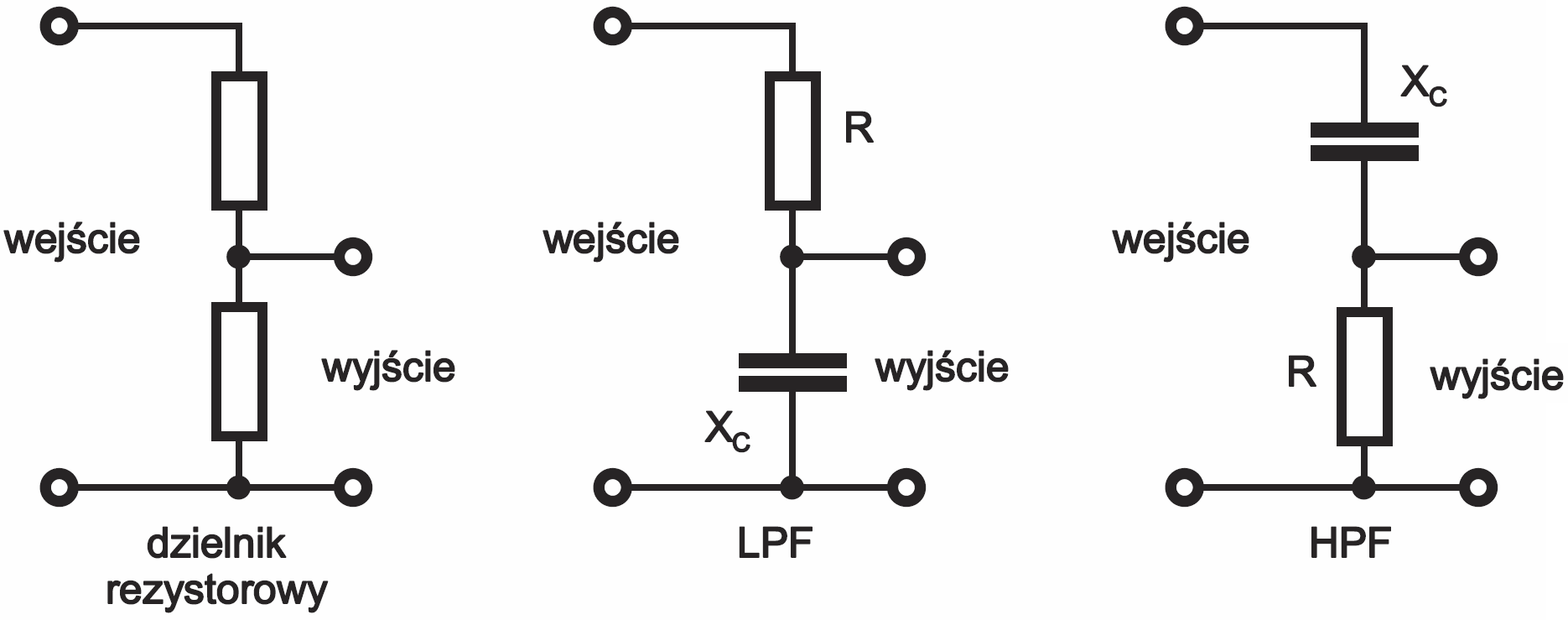
Możemy śmiało potraktować takie filtry jako dzielniki napięcia według rysunku 3. Przykładowo w filtrze dolnoprzepustowym (LPF) przy bardzo małych częstotliwościach reaktancja kondensatora X_C jest bardzo duża, wielokrotnie większa od rezystancji R, i możemy uznać, że kondensator ten w ogóle nie ma wtedy znaczenia – przebiegi o małych częstotliwościach przechodzą przez dzielnik (rezystor) niestłumione. Z kolei przy bardzo dużych częstotliwościach, reaktancja X_C jest bardzo mała, bliska zeru. Oznacza to, że przebiegi o bardzo wysokich częstotliwościach są w filtrze LPF praktycznie zwierane do masy, a przynajmniej bardzo silnie tłumione. I w niektórych zastosowaniach wystarczy takie uproszczone wyobrażenie, że dla przebiegów o dużych częstotliwościach kondensator stanowi zwarcie, a dla prądu stałego i bardzo małych częstotliwości – stanowi przerwę.

Co ważne, dla każdego takiego filtru dolno- i górnoprzepustowego możemy łatwo określić jego częstotliwość charakterystyczną, graniczną. Zapamiętaj raz na zawsze: częstotliwość charakterystyczna filtru RC to częstotliwość, przy której reaktancja kondensatorów ma wartość równą rezystancji. Jeżeli X_C ma się równać R, dla obu filtrów możemy napisać: X_C = 1 / 2 πfC = R i przekształcając obliczyć częstotliwość graniczną: f = 1 / 2πRC

W praktyce często podstawiamy przybliżoną wartość 1/2π=0,16 i wykorzystujemy postać: f = 0,16 / RC pamiętając, że jeśli R, C wyrazimy w omach i faradach, to częstotliwość wyjdzie w hercach.

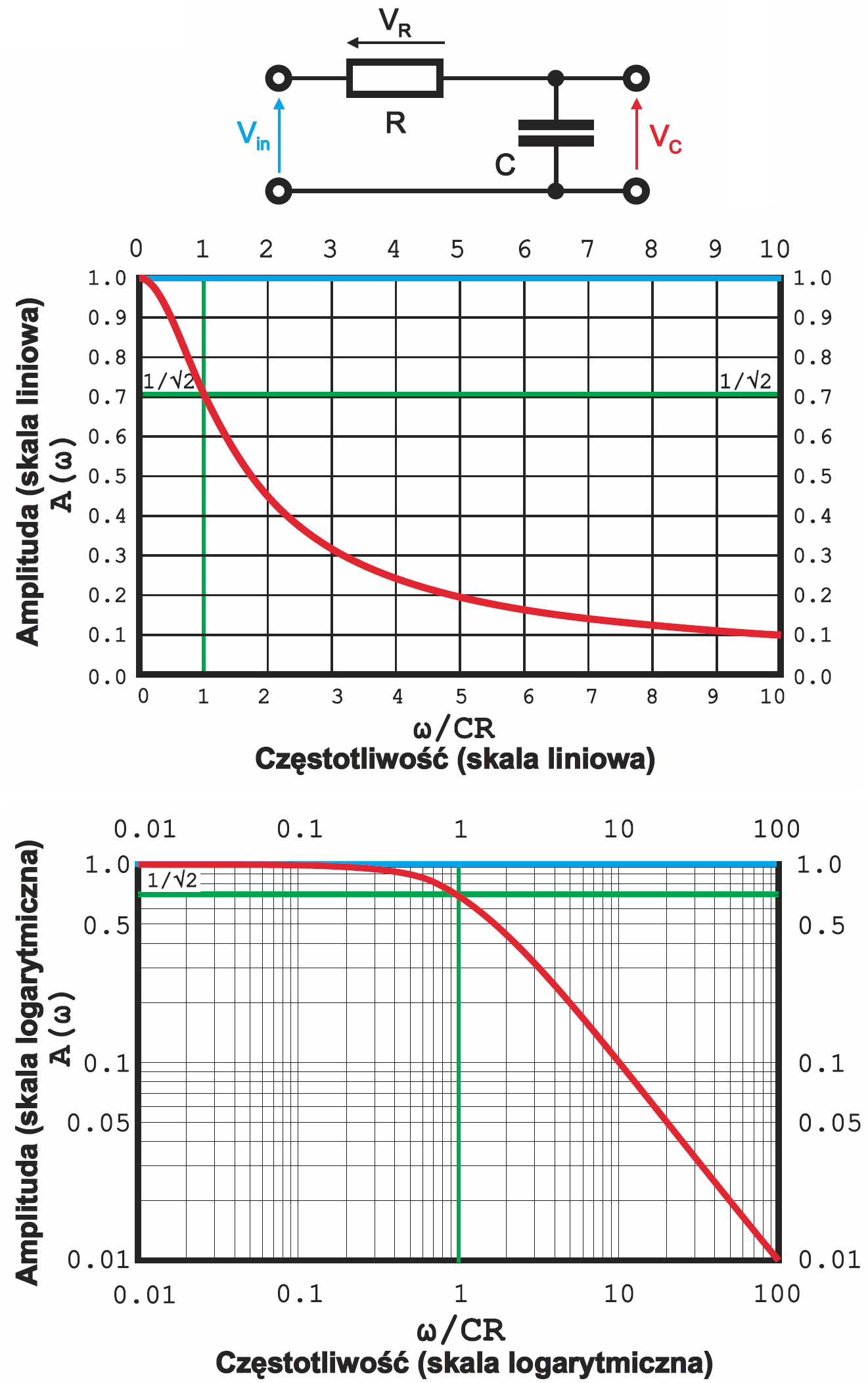
Łatwo obliczyć częstotliwość graniczną, jednak zazwyczaj interesuje nas charakterystyka filtru w zakresie „pośrednim”, przejściowym, w pobliżu tej częstotliwości granicznej. Rysunek 1 wcale nie sugeruje, że kondensator będzie pełnić rolę skutecznego filtru. Jednak nie jest aż tak źle. Rysunek 4 pokazuje filtr dolnoprzepustowy i jego charakterystykę przenoszenia w funkcji częstotliwości. Oba dolne wykresy pokazują tę samą charakterystykę, tylko wykres z rysunku 4b przedstawiony jest w skali liniowej, a z rysunku 4c – w skali logarytmicznej.

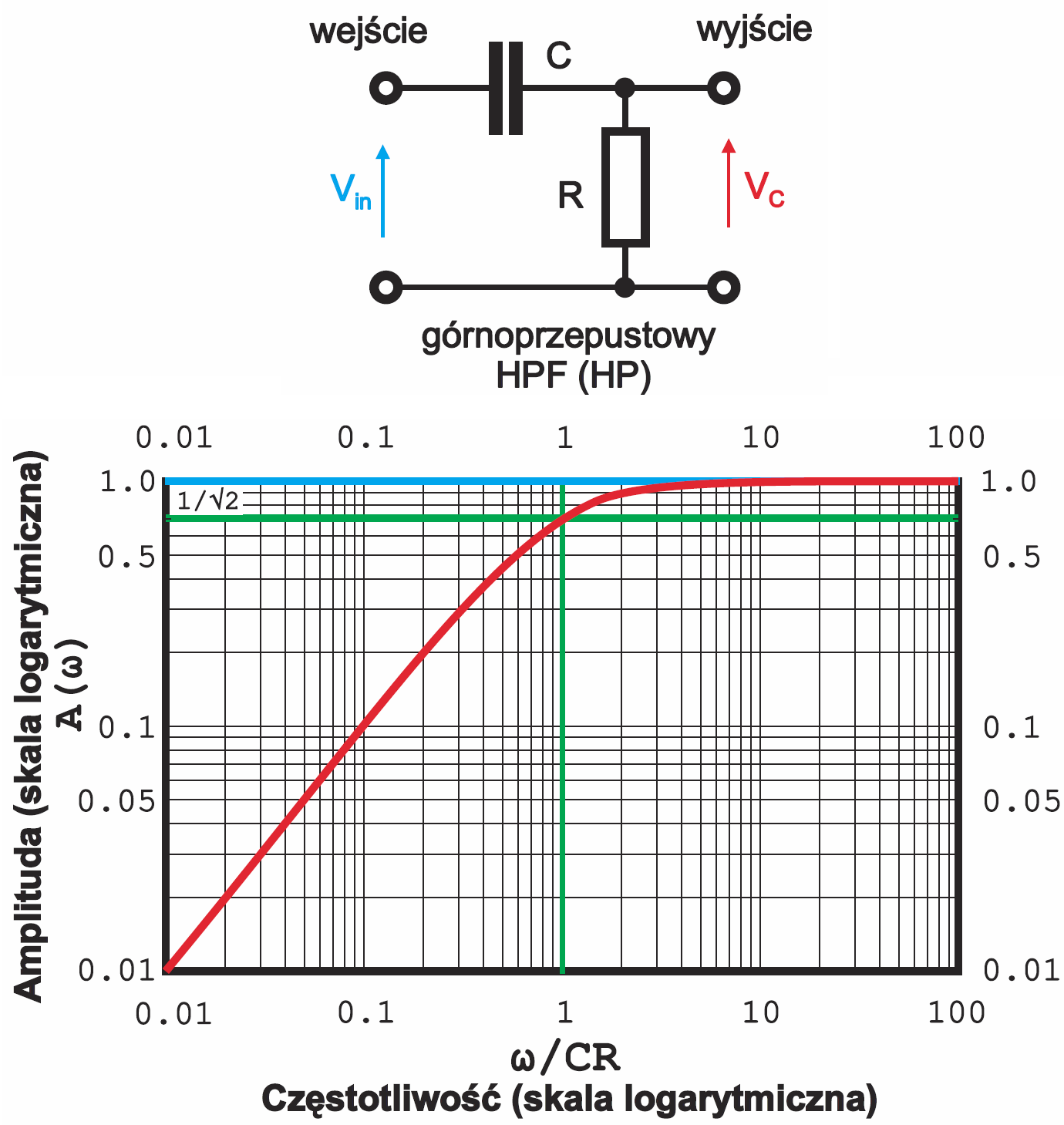
Dla porządku dodam, że filtr górnoprzepustowy (HPF) ma „logarytmiczną” charakterystykę przenoszenia jak na rysunku 5.

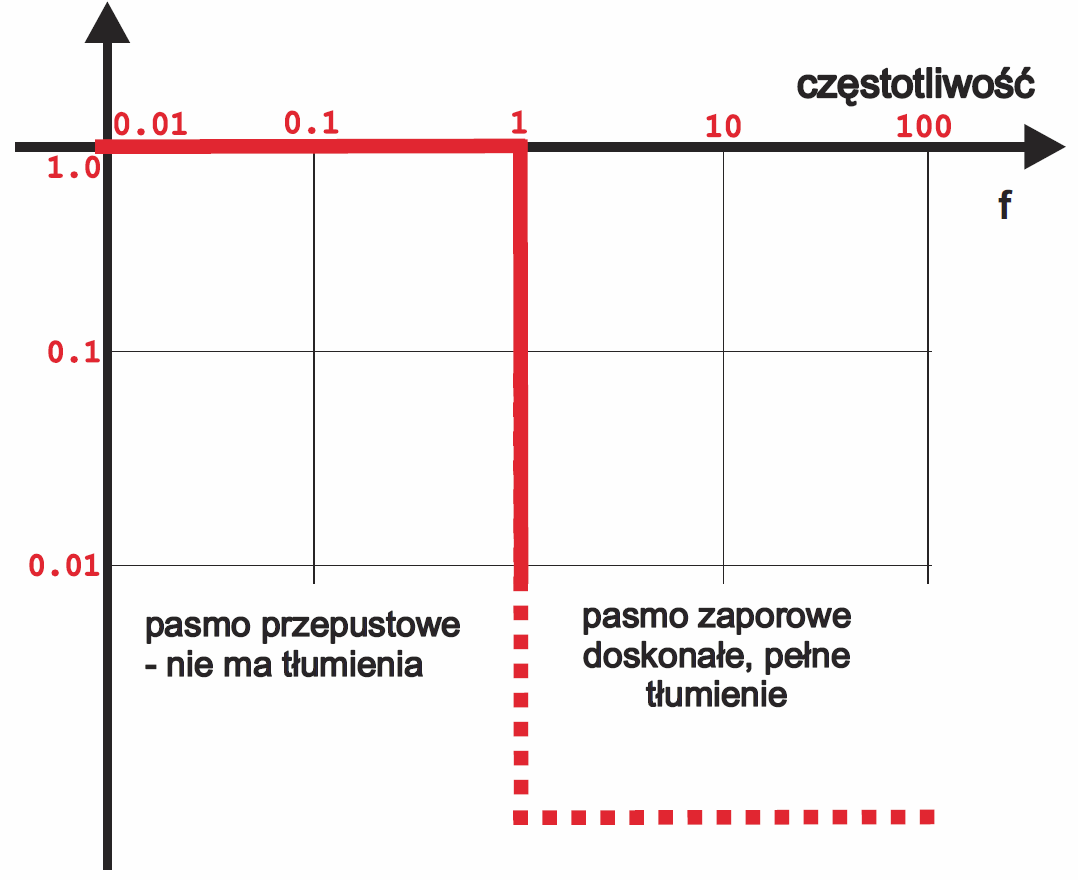
Charakterystyki w skali logarytmicznej są nie tylko „ładniejsze”, ale też lepiej odzwierciedlają różne aspekty naszej rzeczywistości, w tym właściwości ludzkiego słuchu czy wzroku. Dlatego w elektronice często wykorzystujemy charakterystyki w skali logarytmicznej. Wykresy z rysunków 4 i 5 świadczą, że obwód RC istotnie jest filtrem, choć daleko mu do ideału, ponieważ stromość opadania charakterystyki jest niewielka. Przy dziesięciokrotnej (o dekadę) zmianie częstotliwości tłumienie zmienia się dziesięciokrotnie (czyli o 20 dB). Podobnie dwukrotna (o oktawę) zmiana częstotliwości powoduje zmianę tłumienia dwukrotną, czyli o 6 dB. Dlatego mówimy, że stromość takich prostych filtrów RC wynosi 20 dB/dekadę, czyli 6 dB/oktawę. Idealny filtr miałby charakterystykę jak na rysunku 6 – takich filtrów nie ma, ale skomplikowane i rozbudowane filtry mogą mieć stromość opadania charakterystyki ponad 100 dB na dekadę.

Zapewne zauważyłeś, że choć przy częstotliwości granicznej rezystancja R ma wartość liczbową równą reaktancji X_C, jednak omawiane filtry nie tłumią wtedy sygnału dwukrotnie jak byłoby to w przypadku dwóch jednakowych rezystorów. W poprzednich odcinkach szczegółowo wałkowaliśmy temat reaktancji kondensatora i przesunięcia fazy. Właśnie z uwagi na to przesuniecie fazy, przy częstotliwości granicznej filtr RC tłumi sygnał 1,41-krotnie (ściśle: pierwiastek z dwóch). Inaczej mówiąc, przy częstotliwości granicznej sygnał wyjściowy ma 0,707 wartości sygnału wejściowego, czyli w przybliżeniu 71% sygnału wejściowego. W mierze logarytmicznej oznacza to spadek o 3 dB. Zapamiętaj, że przy częstotliwości granicznej filtr tłumi sygnał o 3 dB. Kwestie przesunięcia fazy na razie pomijamy.

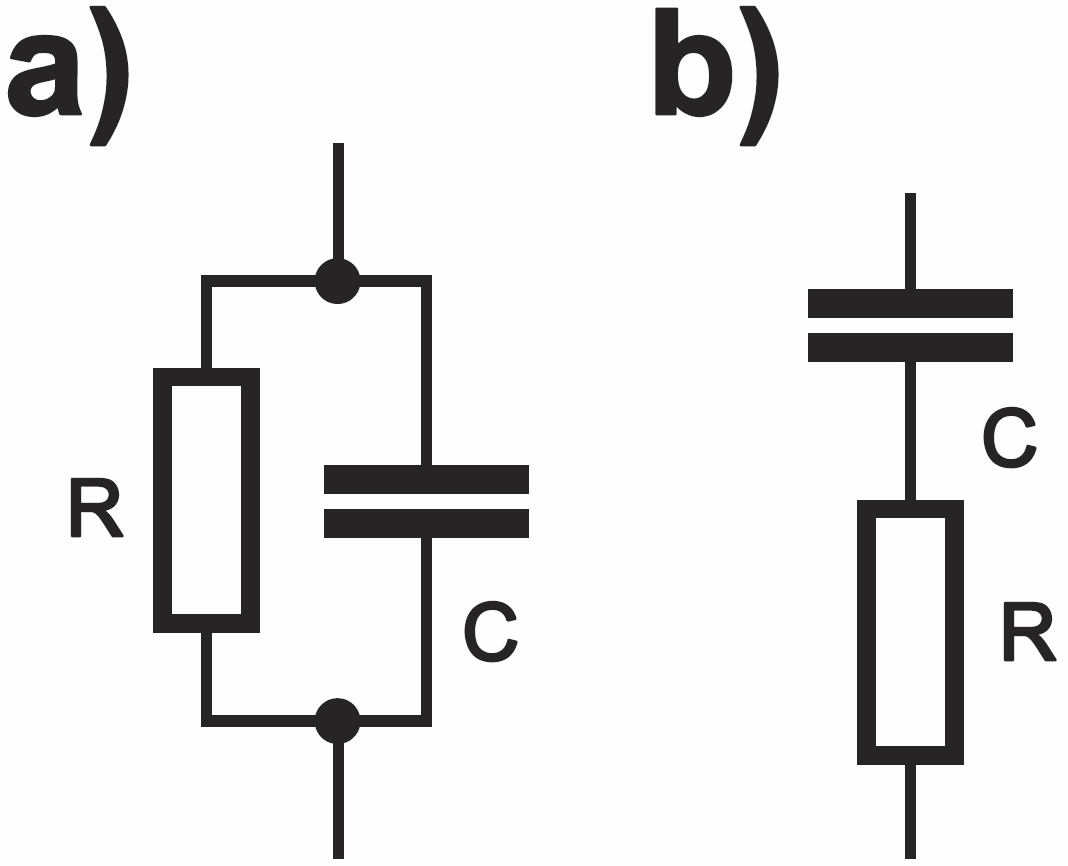
I jeszcze jedna sprawa. W praktyce oprócz klasycznych filtrów według rysunku 2, mamy też do czynienia po prostu z równoległym lub szeregowym połączeniem elementów RC – patrz przykład na rysunku 7. Takie obwody RC nie są dzielnikami napięcia, ale w sumie też mają właściwości filtru, ponieważ ich oporność wypadkowa zależy od częstotliwości.

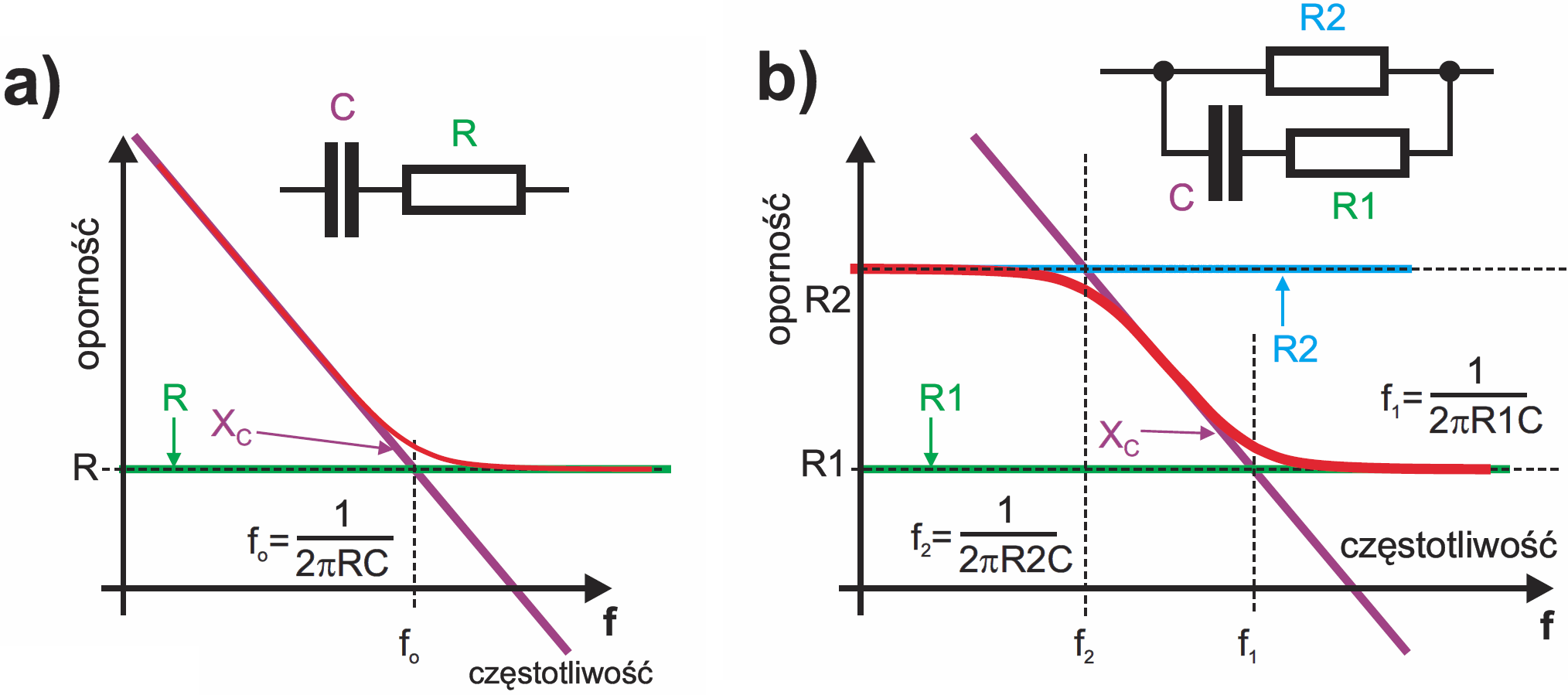
W tych przypadkach również interesuje nas częstotliwość graniczna, przy której reaktancja X_C jest równa rezystancji R – tu też korzystamy ze wzoru f = 1 / 2πRC. Na przykład oporność obwodu z rysunku 7a przy bardzo małych częstotliwościach jest praktycznie równa rezystancji R, natomiast przy dużych częstotliwościach oporność wypadkowa jest praktycznie równa X_C, czyli dąży do zera. Wykres oporności takiego obwodu wyglądałby jak na rysunku 4. Natomiast w obwodzie szeregowym przy małych częstotliwościach oporność jest duża, wyznaczona przez X_C, a przy dużych częstotliwościach reaktancja X_C jest bardzo mała i oporność wypadkowa jest praktycznie równa rezystancji R. Wykres oporności takiego szeregowego obwodu wygląda jak na rysunku 8a (linia czerwona). Jeśli do takiego obwodu dołączymy rezystor R2 o rezystancji większej niż R1, to przebieg oporności wypadkowej będzie wyglądał mniej więcej jak na rysunku 8b. Celowo używam określenia oporność wypadkowa. Ściślej biorąc, należałoby mówić o impedancji i module impedancji, a także o kącie przesunięcia fazy. Na razie kwestię przesunięcia fazy pomijamy.

Zapamiętaj raz na zawsze, że w prostych obwodach RC częstotliwość charakterystyczną obliczamy ze wzoru:

f = 1 / 2 πRC lub f = 0,16 / RC

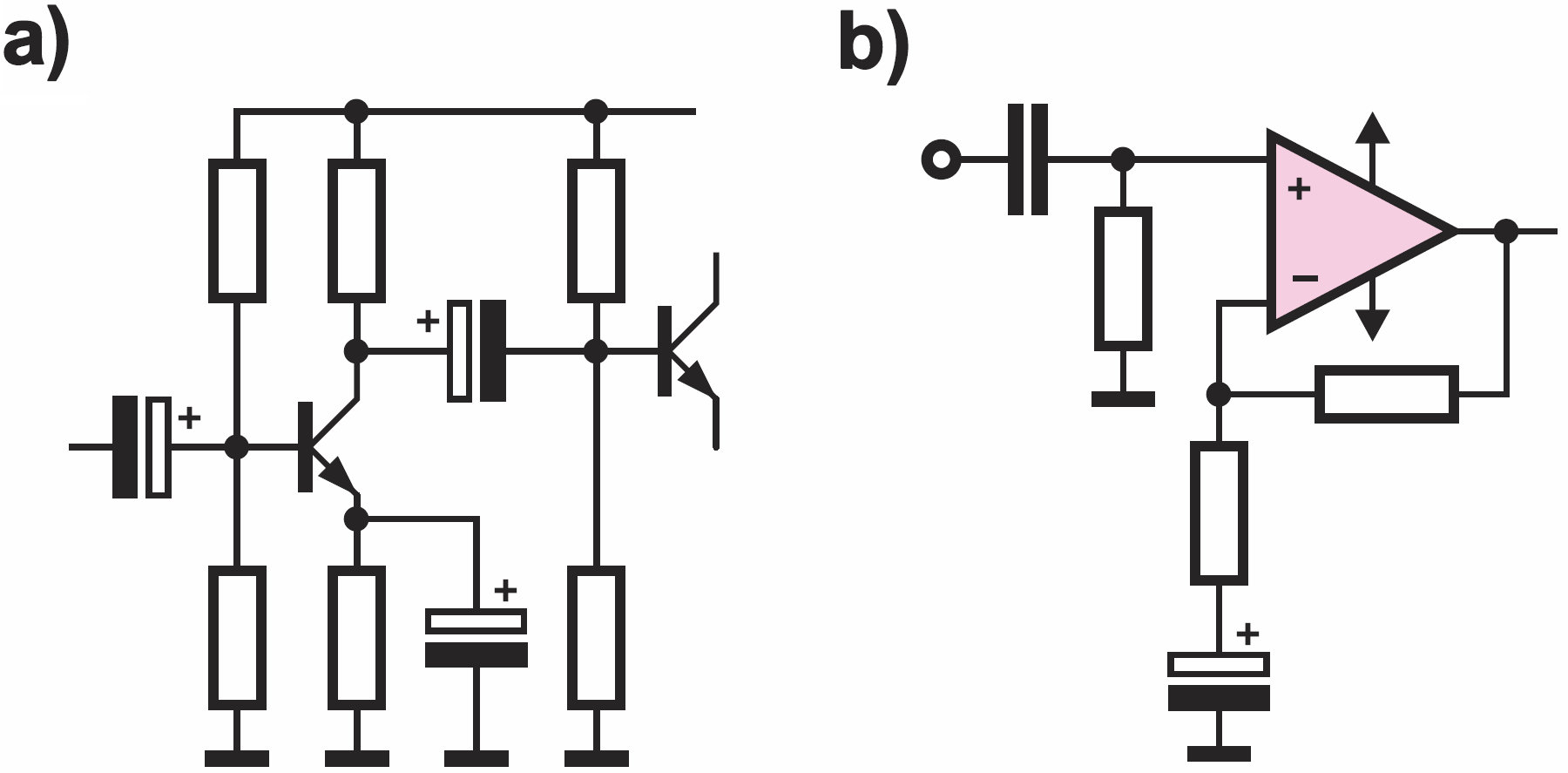
W praktyce mamy w układach mnóstwo obwodów RC, pełniących rolę filtrów. W wielu wypadkach moglibyśmy mówić też o filtrach górnoprzepustowych (HPF) i dolnoprzepustowych (LPF), ale czasem radykalnie upraszczamy sprawę i interesuje nas tylko to, że kondensator dla prądów stałych stanowi przerwę, a dla przebiegów zmiennych stanowi zwarcie. Ewentualnie co najwyżej interesuje nas reaktancja kondensatora dla najniższej częstotliwości pracy. A często nie zastanawiamy się nad reaktancją X_C, stosujemy z zapasem większy kondensator i istotne jest tylko to, że kondensator przepuszcza przebiegi zmienne i oddziela obwody, gdzie panują różne napięcia stałe. Na rysunku 9 masz dwa przykłady z układów audio.

W omówionych właśnie przypadkach zjawisko magazynowania energii nie ma dla nas żadnego znaczenia – interesuje nas tylko to, że kondensator pracuje w układzie filtru. W następnym odcinku spojrzymy na kondensatory z lotu ptaka.

Piotr Górecki